Dear community,

I am having trouble in solving a non-linear, coupled system of equations to describe diffusion-controlled bubble growth in a viscoelastic medium.
The problem is described in detail https://pubs.acs.org/doi/abs/10.1021/ie060295a .
The equation I am trying to solve in time domain (t={0,0.01}) is:

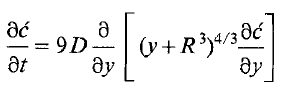
Where c'=c-c0, D is the diffusion coefficient and R is the bubble radius.
The initial and boundary conditions are:

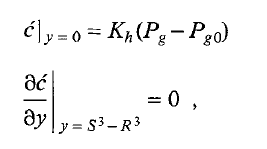
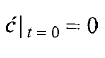
Where Kh is a constant, Pg is a pressure computed from the momentum balance, Pg0 is the initial pressure in the bubble (constant) and S is the radius of the bubble shell.

My way of solving it using NDsolve and implicit Runge Kutta method looks like the following:

CR=Kh*P;
CR0=Kh*P0
R=10^-6;
Rshell=20*10^-6;

concprof = NDSolve[{D[conc[y, t], t] == 9*Diff*D[(y + R^3)^(4/3)*D[conc[y, t], y], y],
  conc[y, 0] == 0,
   (conc[0, t] /. t ->0.01) == CR-C0,
   Derivative[1, 0][conc][(Rshell^3 - R^3), t] == 0},
  conc,
  {y, 0, (Rshell^3 - R^3)},
  {t,0, 0.01},
  Method -> "ImplicitRungeKutta"]

If doing so, I get "Boundary condition conc[0,0.01]==-0.0222257 is not specified on a single edge of the boundary of the computational domain."

If I try in alternative:

concprof = NDSolve[{D[conc[y, t], t] == 9*Diff*D[(y + R^3)^(4/3)*D[conc[y, t], y], y],
  conc[y, 0] == 0,
   conc[0, t]== CR-C0,
   Derivative[1, 0][conc][(Rshell^3 - R^3), t] == 0},
  conc,
  {y, 0, (Rshell^3 - R^3)},
  {t,0, 0.01},
  Method -> "ImplicitRungeKutta"]

I get NDSolve::ibcinc: Warning: boundary and initial conditions are inconsistent.

Can someone help me understand what I am doing wrong?

Thanks!