It's well known that optimal logarithmic times for memory management functions such as Insert and Delete can be achieved by implementing hyperbolic data structures, usually trees. A SkipList is a competitive alternative to a search tree, which (in deterministic form) can utilize a hierarchy of linked lists to emulate B-tree update dynamics. SkipLists are inherently multicomputational, because typical trajectories through update space usually take the SkipList to a non-canonical form. While it may be interesting to study confluence of SkipList update sequences, our primary motivation for implementing SkipLists is to later apply them to optimize simulations of hard square or hard sphere collisions. We will compare performance statistics with another similar experimental function IndexedQueue.

The basic idea behind all hyperbolic optimizations is already present in a simple binary search. We don't need to write our own implementation of binary search code, because this question has already been answered time and again on stack exchange. Here's a nice one from Leonid Shifrin:

InsertPosition[list_List, elem_
   ] := Module[{n0 = 1, n1 = Length[list], m},
   While[n0 <= n1, m = Floor[(n0 + n1)/2];
    If[list[[m]] == elem,
     While[list[[m]] == elem, m++]; Return[m]];
    If[list[[m]] < elem, n0 = m + 1, n1 = m - 1]];
   If[list[[m]] < elem, m + 1, m]];

We've made slight changes, and decided to call the function by a name according to its intended use. The next line of code folds through a list of random data and builds a sorted list one item at a time (while recording absolute times at each step):

naiveTimes = Reap[Module[{res},
    Fold[CompoundExpression[
       Sow[AbsoluteTiming[
          res = Insert[#1, #2,
            InsertPosition[#1, #2]]
          ][[1]]], res] &,
     {-Infinity, Infinity},
     RandomSample[Range[2^15]]]]];

LessEqual @@ naiveTimes[[1]]

Out[]= True

ListPlot[naiveTimes[[2]]]

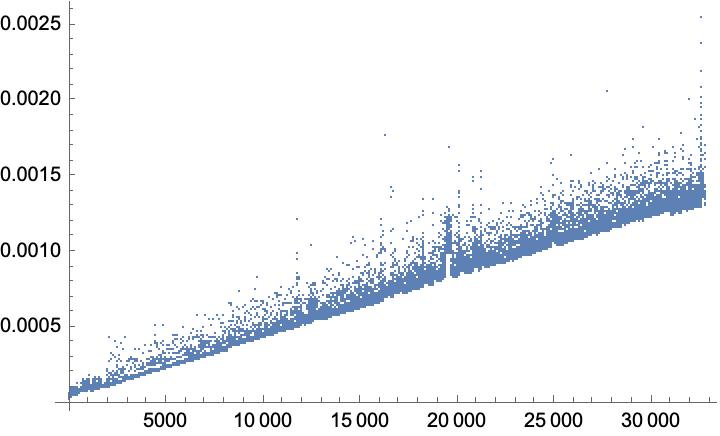
The trend is ultimately linear, because each insertion incurs the cost of copying all elements into a new list of length n + 1. Considering that searching is much faster than insertion, the linear trend seems quite possibly non-optimal. The problem of reducing memory operations to logarithmic times is one that inspired quite a lot of research in the previous century (ha ha!). A summary of results is available here.

The table at bigocheatsheet.com (and many other references elsewhere) compares SkipLists to many different types of trees, and in worst case scenarios, tree-based algorithms are reported to be more reliable. However, this table must assume randomized insertion and deletion, because other authors have shown that SkipLists can emulate B-Tree dynamics if they are given deterministic update rules. This sounds great, but as the algorithm is more obscure and more difficult, we can't just copy a one-liner from stack exchange! In order to see it work in practice, we need to do some serious mathematical analysis, and then write the code.

The exact definition of a B-tree is not necessary in the present discussion of SkipLists, and neither is the functional isomorphism from one structure to another (but you can find it in Knuth's "Art of Computer Programming"). What really matters is local constraints placed on the data structure. Before getting to those, let us briefly discuss the basic dimensions of a SkipList. Roughly speaking, a SkipList of length $n$ is something like a sparse array of dimensions $log(n) \times n$. The bottom row will be completely full of list elements. Each next higher row copies up between $1/2$ and $1/k$ of the elements from the proceeding row. For 1,2-SkipLists in particular, we have $k=3$.

How do we decide which elements to promote up the levels? There are many equivalent choices, and we consider them all roughly equal as long as they satisfy these specific local constraints: (1) If a list element goes up a row, neither of it's neighbors can, (2) If an element doesn't go up a row, one of it's neighbors must. Another way to say this is: between any two elements that go up a level, we must find either one or two elements which don't go up. Additionally, we require that the first and last elements of the list should be fixed to $\pm \infty$, and those values go up every level. Here is an example of the structure we're trying to build:

With[{skiplistArray = Append[Prepend[
       PrintValues[inspectionTest, #], -\[Infinity]], \[Infinity]] & /@
     Range[4]},
 GraphicsRow[Show[#, ImageSize -> 300] & /@ {
    ArrayPlot[Reverse[Normal[SparseArray[
        Flatten[MapIndexed[Function[{row, ind},
           Map[{ind[[1]], Position[
                 skiplistArray[[1]]
                 , #][[1, 1]]} -> # &, row]],
          skiplistArray]]]]],
     ColorRules -> {0 -> Lighter@Blue},
     AspectRatio -> 0.8, Mesh -> True],
    Skip12Graph@inspectionTest}, 15]]

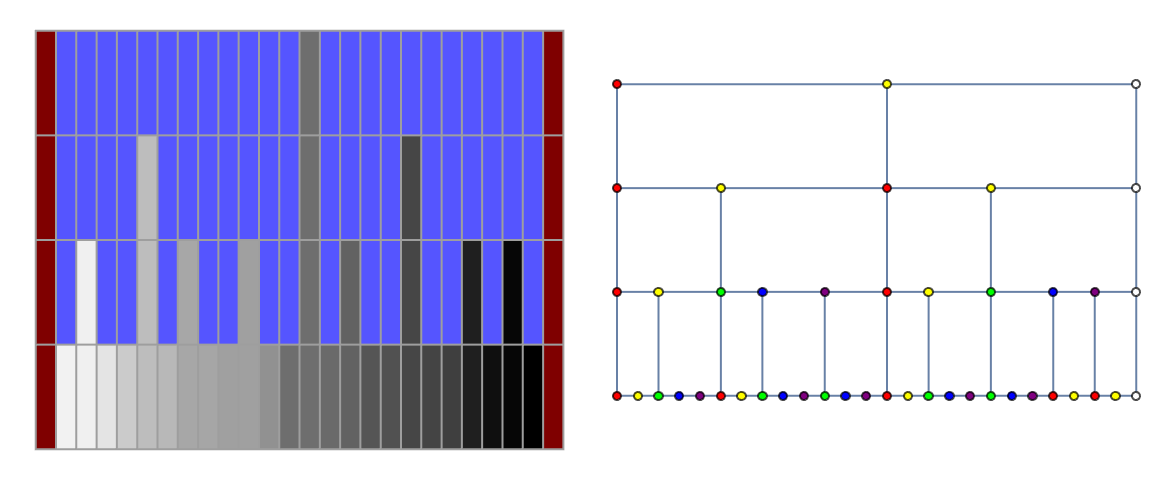
The array form of the SkipList appears on the left, with the following values depicted in grayscale:

PrintValues[inspectionTest]
Out[]= {54, 59, 105, 204, 257, 276, 344, 349, 369, 370, 428, 564, 565, 
             579, 611, 663, 678, 718, 726, 746, 872, 934, 969, 993}

By scanning the array left-to-right, skipping zeros, and comparing values with a search term, dropping down when the next horizontal element is greater than, we find our way by forward and downward steps only to the correct InsertPosition in logarithmic time (complexity follows from the vertical height of the array and the bound of three comparisons per row). However, if we try to insert a value at the InsertPosition, we again encounter the list copying problem, this time for an even larger list!

The graph on the right is easier to search, and can be updated by local operations: adding and / or deleting edges and vertices--easier said than done. Notice that the vertices are colored with five or six colors. Colors indicate the local (oriented) vertex figure, and lead immediately to a five-way case split for insertion and deletion. Deletion of a blue or purple vertex is always easy, as is insertion next to a yellow vertex. Insertion next to blue or purple requires slightly more thought. Furthermore, deleting a red vertex is more difficult than deleting a green vertex, while deleting a yellow vertex leads to hair-pulling subcases.

Unfortunately, we don't have time for a detailed explanation exactly how the update functions are derived, and (as usual?) we will have to settle for "proof in practice". An empty SkipList is represented as follows:

InitializeSkip12[] = <|"Depth" -> 0,
   "Data" -> <|0 -> <|"Value" -> -\[Infinity]|>, -1 -> <|"Value" -> \[Infinity]|>|>,
   "MissingIndices" -> <||>,
   "NextIndex" -> 1,
   "KeyToIndex" -> <||>,
   "IndexToKey" -> <||>
   |>;

And then a SkipList with one element 1 is:

InitializeSkip12[data_Association
  ] := Fold[
  Function[{skip12, key, value},
     Skip12Insert[skip12, key, value]
     ][#1, #2[[1]], #2[[2]] ] &,
  InitializeSkip12[],
  Transpose[{
    Keys[data], Values[data]
    }]]

InitializeSkip12[Association[k[1] -> 1]]

Out[] = <|"Depth" -> 1, "Data" -> <|
    0 -> <|"Value" -> -\[Infinity], 1 -> <|"+" -> 1, "t" -> 1|>|>,
    -1 -> <|"Value" -> \[Infinity], 1 -> <|"-" -> 1|>|>,
    1 -> <|"Value" -> 1, 1 -> <|"-" -> 0, "+" -> -1, "t" -> 2|>
      |>|>,
  "MissingIndices" -> <||>,
  "NextIndex" -> 2,
  "KeyToIndex" -> <|k[1] -> 1|>,
  "IndexToKey" -> <|1 -> k[1]|>
  |>

Values are assumed to be numeric SortBy scores, and the Keys can be arbitrary expressions, either unique or uniquified. Initialization of a SkipList from unsorted input data depends on insert functions, the first of which is very similar to earlier InsertPosition:

InsertPosition[skip12_, val_
  ] := Module[{depth, data, cursor, next},
  depth = skip12["Depth"];
  data = skip12["Data"];
  cursor = 0;
  While[depth > 0,
   If[data[next = data[cursor, depth, "+"], "Value"] > val,
    depth--,
    cursor = next
    ]
   ];
  {cursor, data[cursor, 1, "+"]}
  ]

Skip12Insert[skip12_, key_, value_
  ] := Module[{nextSkip12 = skip12, index, left, right},
  If[! TrueQ[Lookup[skip12["KeyToIndex"], key, True]],
   (* message here? *)
   Return[$Failed]];
  (* check value type? *)
  If[TrueQ[index = First[skip12["MissingIndices"], True]],
   index = skip12["NextIndex"];
   nextSkip12["NextIndex"] = nextSkip12["NextIndex"] + 1,
   nextSkip12["MissingIndices"] = 
    KeyDrop[skip12["MissingIndices"], index]
   ];
  nextSkip12["Data", index] = Association[
    "Value" -> value,
    1 -> Association[]
    ];
  nextSkip12["KeyToIndex", key] = index;
  nextSkip12["IndexToKey", index] = key;
  If[skip12["Depth"] == 0,
   nextSkip12["Depth"] = 1;
   nextSkip12["Data", 0, 1] = Association["+" -> index, "t" -> 1];
   nextSkip12["Data", -1, 1] = Association["-" -> index];
   nextSkip12["Data", index, 1] = 
    Association["-" -> 0, "+" -> -1, "t" -> 2]
   ,
   {left, right} = InsertPosition[skip12, value];
   nextSkip12 = Skip12Insert[nextSkip12, index, left, right, 1]
   ];
  nextSkip12
  ]

Skip12Insert[skip12_, index_, left_, right_, level_
  ] := Module[{nextSkip12 = skip12, types,
   reassign, nextTypes, end,
   left2, left3, right2},
  nextSkip12["Data", left, level, "+"] = index;
  nextSkip12["Data", right, level, "-"] = index;
  nextSkip12["Data", index, level, "+"] = right;
  nextSkip12["Data", index, level, "-"] = left;
  types = skip12["Data", #, level, "t"] & /@ {left, right};
  Set[{reassign, nextTypes},
   Switch[types,
    {1, 2},
    {{left, index, right}, {3, 4, 5}},
    {2, _},
    left2 = nextSkip12["Data", left, level, "-"];
    {{left2, left, index}, {3, 4, 5}},
    {3, 4},
    right2 = nextSkip12["Data", right, level, "+"];
    {{left, index, right, right2}, {1, 2, 1, 2}},
    {4, 5},
    left2 = nextSkip12["Data", left, level, "-"];
    {{left2, left, index, right}, {1, 2, 1, 2}},
    {5, _},
    left2 = nextSkip12["Data", left, level, "-"];
    left3 = nextSkip12["Data", left2, level, "-"];
    {{left3, left2, left, index}, {1, 2, 1, 2}}
    ]];
  MapThread[
   Set[nextSkip12["Data", #1, level, "t"], #2] &,
   {reassign, nextTypes}];
  If[Length[nextTypes] == 4,
   If[skip12["Depth"] == level,
    nextSkip12["Depth"] = level + 1;
    end = nextSkip12["Data", reassign[[4]], level, "+"];
    nextSkip12["Data", 0, level + 1] = Association[
      "+" -> reassign[[3]], "t" -> 1];
    nextSkip12["Data", reassign[[3]], level + 1] = Association[
      "-" -> 0, "+" -> end, "t" -> 2];
    nextSkip12["Data", end, level + 1] = Association[
      "-" -> reassign[[3]] ]
    ,
    nextSkip12["Data", reassign[[3]], level + 1] = Association[];
    nextSkip12 = Skip12Insert[
      nextSkip12, reassign[[3]],
      First[reassign],
      nextSkip12["Data", First[reassign], level + 1, "+"],
      level + 1]
    ]];
  nextSkip12
  ]

Then we have Delete functions, including one monstrous Skip12KeyDrop2 for the tricky yellow vertices:

Skip12ShiftVertical[skip12_, shiftFrom_, shiftTo_, level_
  ] := Module[{nextSkip12 = skip12, nextLevel, levelData},
  nextLevel = level + 1;
  While[! TrueQ[levelData = Lookup[
       skip12["Data", shiftFrom], nextLevel,
       True]],
   nextSkip12["Data", shiftFrom] = KeyDrop[
     nextSkip12["Data", shiftFrom], nextLevel];
   nextSkip12["Data", shiftTo, nextLevel] = levelData;
   nextSkip12["Data", levelData["+"], nextLevel, "-"] = shiftTo;
   nextSkip12["Data", levelData["-"], nextLevel, "+"] = shiftTo;
   nextLevel++];
  nextSkip12
  ]

Skip12KeyDrop[1][skip12_, key_, level_, left_, right_
  ] := Module[{nextSkip12 = skip12, left2, left3,
   nextLevel, levelData},
  (*Echo[1->level];*)
  left2 = skip12["Data", left, level, "-"];
  If[SameQ[skip12["Data", left, level, "t"], 2],
   (* recurse *)
   MapThread[Set[nextSkip12["Data", #1, level, "t"], #2] &,
    {{left2, left, right}, {3, 4, 5}}];
   If[level == skip12["Depth"], nextSkip12,
    Skip12KeyDrop[nextSkip12, key, level + 1]]
   ,
   (* merge *)
   left3 = skip12["Data", left2, level, "-"];
   MapThread[Set[nextSkip12["Data", #1, level, "t"], #2] &,
    {{left3, left2, left}, {1, 2, 1}}];
   Skip12ShiftVertical[nextSkip12, key, left, level]
   ]
  ]

Skip12KeyDrop[2][skip12_, key_, level_, left_, right_
  ] := Module[{nextSkip12 = skip12,
   left2, left3, left4, right2, right3,
   nextLevel, levelData},
  (*Echo[2->level];*)
  left2 = skip12["Data", left, level, "-"];
  Which[
   (* topped out *)
   And[left == 0, SameQ[Infinity,
     skip12["Data", right, "Value"]  ] ],
   nextSkip12["Data", left] = KeyDrop[nextSkip12["Data", left], level];
   nextSkip12["Data", right] = 
    KeyDrop[nextSkip12["Data", right], level];
   nextSkip12["Depth"] = nextSkip12["Depth"] - 1
   ,
   (* merge right *)
   SameQ[skip12["Data", right, level, "t"], 3],
   right2 = skip12["Data", right, level, "+"];
   right3 = skip12["Data", right2, level, "+"];
   MapThread[Set[nextSkip12["Data", #1, level, "t"], #2] &,
    {{right, right2, right3}, {2, 1, 2}}];
   nextSkip12 = Skip12ShiftVertical[
     nextSkip12, right, right2, level]
   ,
   (* merge left *)
   SameQ[skip12["Data", left2, level, "t"], 5],
   left3 = skip12["Data", left2, level, "-"];
   left4 = skip12["Data", left3, level, "-"];
   MapThread[Set[nextSkip12["Data", #1, level, "t"], #2] &,
    {{left4, left3, left2, left}, {1, 2, 1, 2}}];
   nextSkip12 = Skip12ShiftVertical[
     nextSkip12, left, left2, level]
   ,
   (* recurse right *)
   UnsameQ[Infinity, nextSkip12["Data", right, "Value"]],
   right2 = skip12["Data", right, level, "+"];
   MapThread[Set[nextSkip12["Data", #1, level, "t"], #2] &,
    {{left, right, right2}, {3, 4, 5}}];
   If[level != skip12["Depth"], Set[nextSkip12,
     Skip12KeyDrop[nextSkip12, right, level + 1]]]
   ,
   (* recurse left *)
   True, 
   left3 = skip12["Data", left2, level, "-"];
   MapThread[Set[nextSkip12["Data", #1, level, "t"], #2] &,
    {{left3, left2, left}, {3, 4, 5}}];
   If[level != skip12["Depth"], Set[nextSkip12,
     Skip12KeyDrop[nextSkip12, left, level + 1]]]
   ];
  nextSkip12
  ]

Skip12KeyDrop[3][skip12_, key_, level_, left_, right_
  ] := Module[{nextSkip12 = skip12,
   rightright, nextLevel, levelData},
  (*Echo[3->level];*)
  rightright = skip12["Data", right, level, "+"];
  nextSkip12["Data", right, level, "t"] = 1;
  nextSkip12["Data", rightright, level, "t"] = 2;
  Skip12ShiftVertical[
   nextSkip12, key, right, level
   ]]

Skip12KeyDrop[4][skip12_, key_, level_, left_, right_
  ] := Module[{nextSkip12 = skip12},
  (*Echo[4->level];*)
  nextSkip12["Data", left, level, "t"] = 1;
  nextSkip12["Data", right, level, "t"] = 2;
  nextSkip12
  ]

Skip12KeyDrop[5][skip12_, key_, level_, left_, right_
  ] := Module[{nextSkip12 = skip12, leftleft},
  (*Echo[5->level];*)
  leftleft = skip12["Data", left, level, "-"];
  nextSkip12["Data", leftleft, level, "t"] = 1;
  nextSkip12["Data", left, level, "t"] = 2;
  nextSkip12
  ]

Skip12KeyDrop[skip12_, key_
  ] := Module[{nextSkip12, index},
  index = skip12["KeyToIndex", key];
  nextSkip12 = Skip12KeyDrop[skip12, index, 1];
  nextSkip12["Data"] = KeyDrop[nextSkip12["Data"], index];
  nextSkip12["IndexToKey"] = 
   KeyDrop[nextSkip12["IndexToKey"], index];
  nextSkip12["KeyToIndex"] = KeyDrop[nextSkip12["KeyToIndex"], key];
  nextSkip12["MissingIndices", index] = index;
  nextSkip12
  ]

Skip12KeyDrop[skip12_, index_, level_
  ] := Module[{nextSkip12 = skip12, type, left, right},
  type = skip12["Data", index, level, "t"];
  left = skip12["Data", index, level, "-"];
  right = skip12["Data", index, level, "+"];
  nextSkip12["Data", left, level, "+"] = right;
  nextSkip12["Data", right, level, "-"] = left;
  nextSkip12["Data", index] = 
   KeyDrop[nextSkip12["Data", index], level];
  nextSkip12 = 
   Skip12KeyDrop[type][nextSkip12, index, level, left, right];
  nextSkip12
  ]

Up to this point, we have every necessary tool to start using SkipLists in intensive calculations. Before deploying, we need to check times, and before checking times we need to check quality. Here Quality is whether or not each vertex of the SkipList obeys local constraints, and if the data is correctly sorted:

CheckItem[False][_, _, _, _] = False;

CheckItem[1][skip12_, index_, nextType_, level_
  ] := And[nextType == 2,
  Or[level == skip12["Depth"],
   ! TrueQ[Lookup[skip12["Data", index], level + 1, True]]
   ]]

CheckItem[2][skip12_, index_, nextType_, level_
  ] := Or[nextType, MemberQ[{1, 3}, nextType]]

CheckItem[3][skip12_, index_, nextType_, level_
  ] := And[nextType == 4,
  Or[level == skip12["Depth"],
   ! TrueQ[Lookup[skip12["Data", index], level + 1, True]]
   ]]

CheckItem[4][skip12_, index_, nextType_, level_
  ] := Equal[nextType, 5]

CheckItem[5][skip12_, index_, nextType_, level_
  ] := Or[nextType, MemberQ[{1, 3}, nextType]]

CheckItem[skip12_, index_, level_
  ] := Module[{nextItem, nextType},
  If[TrueQ[nextItem = Lookup[
      skip12["Data", index, level],
      "+", True]],
   Return[False]
   ];
  nextType = Lookup[
    skip12["Data", nextItem, level],
    "t", True];
  CheckItem[
    Lookup[skip12["Data", index, level], "t", False]
    ][skip12, index, nextType, level]
  ]

PrintValues[skip12_, level_ : 1
  ] := If[skip12["Depth"] < level, {},
  Reap[NestWhileList[
     (Sow[skip12["Data", #, "Value"]]; 
       Lookup[skip12["Data", #, level], "+", True]) &,
     0, ! TrueQ[#] &]][[2, 1, 2 ;; -2]]]

CheckSkip12[skip12_
  ] := And[AllTrue[Range[skip12["Depth"]],
   Function[level, SameQ[-1, NestWhile[
      (Lookup[skip12["Data", #, level], "+", True]) &,
      0, CheckItem[skip12, #, level] &]]]],
  Less @@ PrintValues[skip12]]

A quick and sufficiently convincing test is to randomize a data list, insert all elements, and then delete them in a different randomized order. We will keep every intermediary state, and run CheckSkip12 on all results:

Skip12InsertionSequence[init_, data_
  ] := FoldList[
  Function[{skip12, key, value},
     Skip12Insert[skip12, key, value]
     ][#1, #2[[1]], #2[[2]] ] &,
  init,
  Transpose[{
    Keys[data], Values[data]
    }]]

Skip12DeletionSequence[init_, keys_
  ] := FoldList[Function[{skip12, key},
   Skip12KeyDrop[skip12, key]
   ], init, keys]

AbsoluteTiming[
 testInsert = Skip12InsertionSequence[InitializeSkip12[],
    Association[RandomSample[MapIndexed[k[#2[[1]]] -> #1 &,
       Range[2^10]]]]
    ];]

Out[]= {0.222407, Null}

AbsoluteTiming[
 testDelete = Skip12DeletionSequence[Last[testInsert],
    RandomSample[k /@ Range[2^10]]];
 ]

Out[]= {0.176781, Null}

AllTrue[testInsert, CheckSkip12]

Out[]= True

AllTrue[testDelete, CheckSkip12]

Out[]= True

In practice, we're more likely to insert about as often as we delete. Thus we should also test a random walk around the final result of repeated insertion:

init = Last[testInsert];

testRandomWalk = NestList[
   If[RandomReal[] < 1/2,
     Skip12KeyDrop[#,
      RandomChoice[Keys[#["KeyToIndex"]]]
      ],
     Skip12Insert[#,
      k[Max[Keys[#["KeyToIndex"]][[All, 1]]] + 1],
      RandomInteger[2^10]
      ]
     ] &, init, 2^8
   ];

AllTrue[testRandomWalk, CheckSkip12]

Out[] = True

randWalkLens = Length[PrintValues[#]] & /@ testRandomWalk;

ListPlot[randWalkLens]

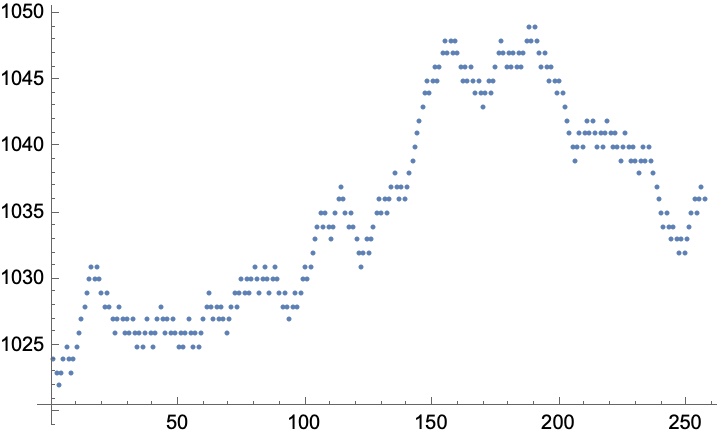
Everything appears to be working perfectly, but we should also do a spot check to visually see that results make sense. To do so we introduce a few utilities that will allow us to expand the first few terms of the multiway graph:

Skip12Graph[skip12_] := Module[{vertices, g1},
  If[skip12["Depth"] == 0,
   Return[Graph[{{-1, 0}, {0, 0}}, {},
     VertexSize -> Large,
     VertexStyle -> {
       {-1, 0} -> White,
       {0, 0} -> Red
       }
     ]]
   ];
  vertices = Function[{level},
     {Lookup[skip12["IndexToKey"], #, #], level
        } & /@ Most[NestWhileList[ Lookup[
          skip12["Data"][#, level], "+", True] &,
            0, ! TrueQ[#] &]]] /@ Range[skip12["Depth"]];
  g1 = GraphUnion[
    Apply[GraphUnion, PathGraph /@ vertices],
    Graph[Catenate[Map[UndirectedEdge[#, # - {0, 1}] &,
       Rest[vertices], {2}]]]];
  Graph[g1,
   VertexStyle -> (# -> Association[
          1 -> Red,
          2 -> Yellow,
          3 -> Green,
          4 -> Blue,
          5 -> Purple,
          0 -> White
          ][Lookup[skip12["Data",
           Lookup[skip12["KeyToIndex"],
            #[[1]], #[[1]]
            ],
           #[[2]]], "t", 0]] & /@ VertexList[g1]),
   VertexSize -> Large,
   VertexCoordinates -> (# -> {
         Position[vertices[[1, All, 1]],
           #[[1]]][[1, 1]], #[[2]]*5
         } & /@ VertexList[g1])]
  ]

CanonicalizeSkip12Graph[g1_
  ] := Module[{g2, vertexRep,
   vertices = VertexList[g1],
   edges = EdgeList[g1]},
  g2 = Graph[vertices, DeleteCases[edges,
     UndirectedEdge[ {z_, x_}, {z_, y_} ] /; And[
       UnsameQ[z, 0], UnsameQ[x, y]]  ]];
  vertexRep = SortBy[# -> {#[[2]] ,
        GraphDistance[g2, {0, 1}, #]
        } & /@ vertices, Last];
  Graph[
   Sort[vertices /. vertexRep],
   Sort[edges /. vertexRep]
   ]]

And these functions are used as:

testSequences = Permutations[MapIndexed[k[#2[[1]]] -> #1 &,
    Range[6]]];

graphSequence = 
  Map[Skip12Graph[#] &, 
     Rest@Skip12InsertionSequence[InitializeSkip12[],
       Association[#]]] & /@ testSequences;

graphSequenceCanonical = Map[CanonicalizeSkip12Graph[#] &,
     #] & /@ graphSequence;

vertexRules = Rule @@@ DeleteDuplicatesBy[
    Transpose[{Catenate[graphSequenceCanonical],
      Catenate[graphSequence]}], First];

multiway = GraphUnion @@ Map[PathGraph[#, DirectedEdges -> True
      ] &, graphSequenceCanonical];

Graph[multiway,
 EdgeStyle -> Gray,
 VertexShapeFunction -> (Inset[#2 /. vertexRules, #1,
     Automatic, #3] &),
 VertexSize -> 1, PerformanceGoal -> "Quality"]

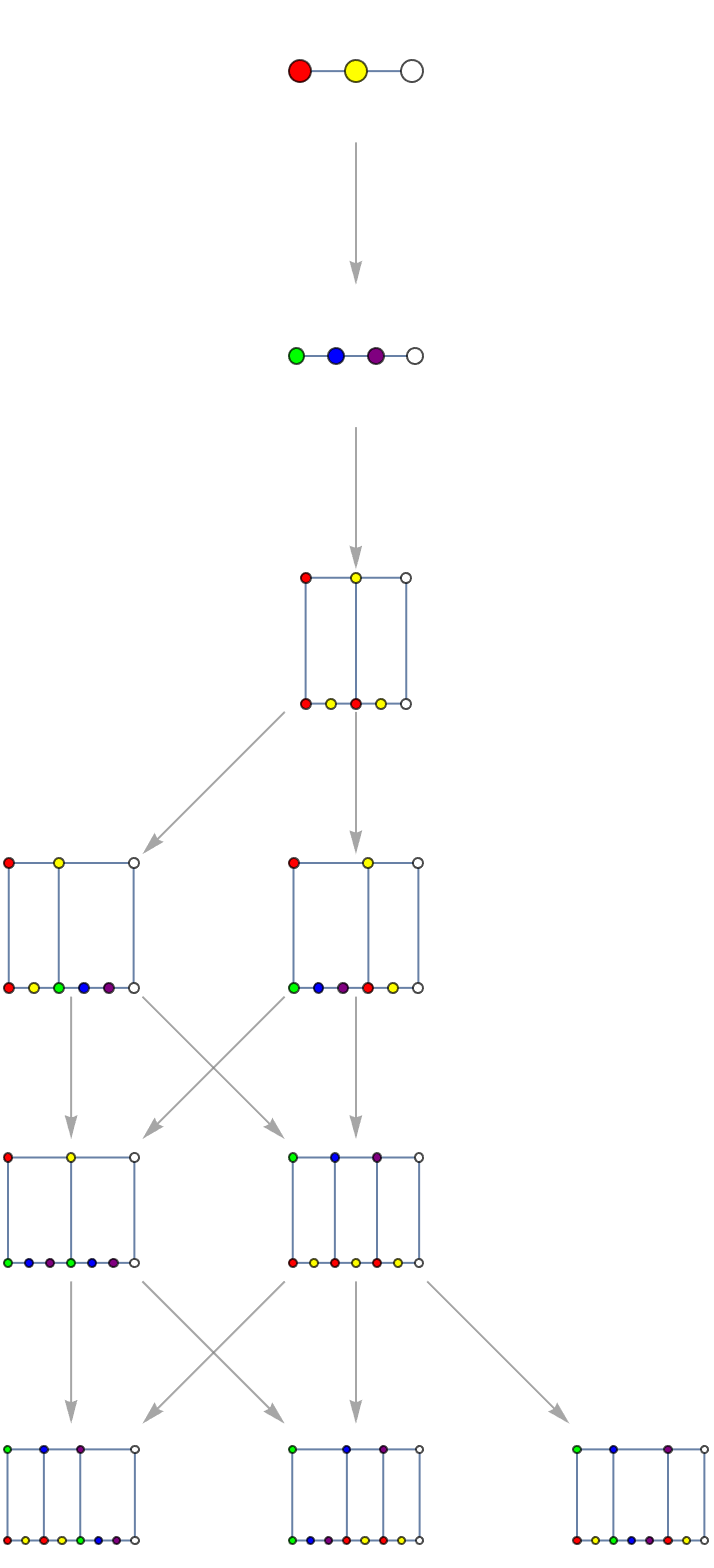
an interesting exercise for students would be to calculate the exact number of SkipLists as a function of list length. Is this integer sequence already in OEIS? I'm guessing it is, but would like to know the number...

Now we can go on to perform timing tests against WFR`IndexedQueue, which provides similar functionality. First we test repeated Insertion:

size = 2^15

SeedRandom[23434];
randData = RandomInteger[size, size];
randKeyedData = MapIndexed[
   {k[#2[[1]]], #1} &, randData
   ];

skiplistInsertionTimes = Reap[Module[{next},
     finalFull = Fold[CompoundExpression[
         Sow[AbsoluteTiming[
            next = Skip12Insert[#1, #2[[1]], #2[[2]]]
            ][[1]]], next] &, InitializeSkip12[],
       randKeyedData]  ]][[2, 1]];


heap = ResourceFunction["IndexedQueue"][
   {"InitialSize" -> 1, "NullElement" -> Missing[],
    "ComparisonFunction" -> Greater},
   {}, "Initialize"];
indexedInsertionTimes = Reap[Module[{next},
     Fold[CompoundExpression[
        Sow[AbsoluteTiming[
           next = ResourceFunction["IndexedQueue"
              ][heap, #2, "Enqueue"]
           ][[1]]], next] &, {},
      randData]  ]][[2, 1]];

heap = ResourceFunction["IndexedQueue"][
   {"InitialSize" -> 1, "NullElement" -> Missing[],
    "ComparisonFunction" -> Greater},
   {}, "Initialize"];

Show[
 ListPlot[MovingAverage[skiplistInsertionTimes, 10]],
 ListPlot[MovingAverage[indexedInsertionTimes, 10],
  PlotStyle -> Orange],
 ListPlot[naiveTimes[[2]], PlotStyle -> Red],
 PlotRange -> All
 ]

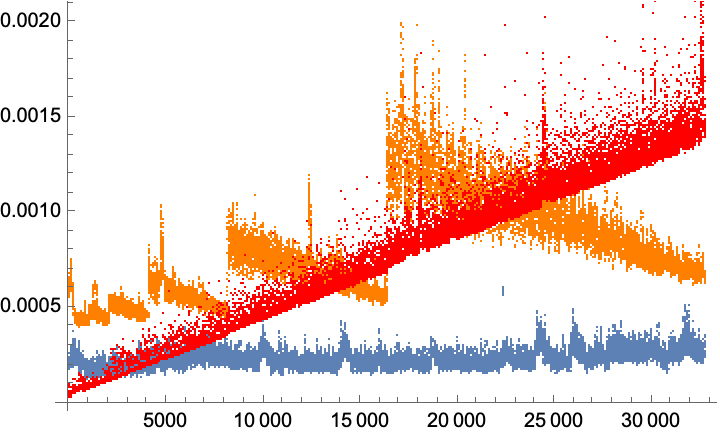
Orange is WFR`IndexedQueue, blue is the new SkipList code, and red is the data from earlier. What's really nice, perhaps even better than absolute height, is that the new algorithm is apparently more stable. This is probably due to the following "details" item from the documentation page:

Generally, an indexed queue is an array of fixed size, so adding and removing elements do not incur memory allocation or deallocation. The one exception is when adding an element to a queue that is at capacity, at which point the heap size is doubled.

The insertion timings graph has great practical importance if / when we decide to deploy logarithmic search as a component to another algorithm such as hard square or hard sphere scattering. It shows that WFR`IndexedQueue can not generally be expected to speed up calculations with fewer than 30,000 list elements ( or possibly pair-interactions of 250+ actors). Compare with new code, where optimization would begin to become noticeable on lists with more than 5000 elements (100+ pairwise actors).

Moving on to the Deletion test, we find what appears to be breakage:

randomKeys = RandomSample[randKeyedData[[All, 1]]];

skiplistDeletionTimes = Reap[Module[{next},
     finalEnd = Fold[CompoundExpression[
         Sow[AbsoluteTiming[
            next = Skip12KeyDrop[#1, #2]
            ][[1]]], next] &, finalFull,
       randomKeys]  ]][[2, 1]];

heap2 = heap;
indexedDeletionTimes = Reap[Module[{next},
     Fold[CompoundExpression[
        Sow[AbsoluteTiming[
           next = ResourceFunction["IndexedQueue"
              ][heap2, #2, "Remove"]
           ][[1]]], next] &, {},
      First /@ randomKeys]  ]][[2, 1]];

Show[
 ListPlot[MovingAverage[skiplistDeletionTimes, 10]],
 ListPlot[MovingAverage[indexedDeletionTimes, 10],
  PlotStyle -> Red],
 PlotRange -> All
 ] 

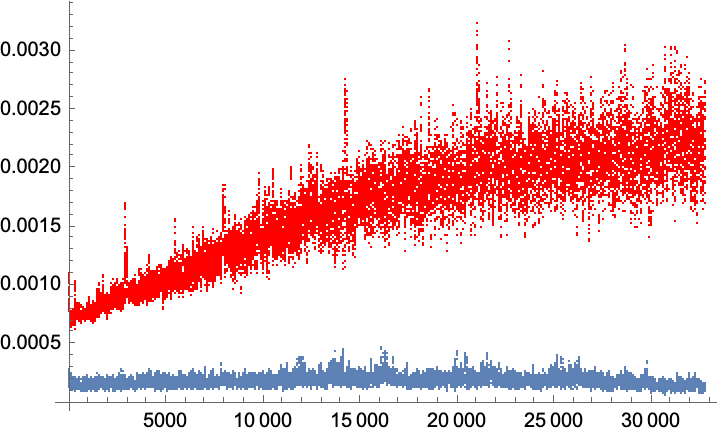
It's possible for WFR`IndexedQueue that deletion times can increase for lists of decreasing length, which clearly violates the $log(n)$ claim. This is apparently a path dependent feature, which leads to bugging, because output length should be zero or thereabout, compare:

KeyDrop[finalEnd, "MissingIndices"]

Out[]= <|"Depth" -> 0,  "Data" -> <|
    0 -> <|"Value" -> -\[Infinity]|>, 
    -1 -> <|"Value" -> \[Infinity]|>
    |>, 
    "NextIndex" -> 32769, 
    "KeyToIndex" -> <||>, 
    "IndexToKey" -> <||>
 |>

Length@DeleteCases[heap2[[1]], Missing[]]

Out[]= 6893

[ This could be my fault If I've misunderstood how to use IndexedQueue, someone please let me know if they can explain this 6893 number!! ]

The data from SkipList also apparently shows some path dependence:

Show[
 ListPlot[MovingAverage[skiplistInsertionTimes, 10],
  PlotStyle -> Green],
 ListPlot[MovingAverage[skiplistDeletionTimes, 10]]
 ]

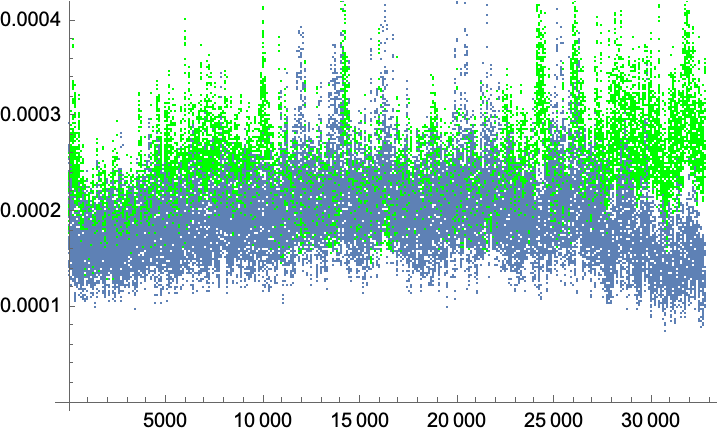
The trend is roughly constant, which can be expected because successive deletions will probably lead to relatively more yellow, red, and green vertices. What's important to notice here is that deletion times are comparable to insertion times, which is what we can reasonably expect. Of course, by compiling, we could probably improve absolute times by an order of magnitude (and I would not be surprised seeing multiple orders of magnitude). Another interesting possibility is threading, but not for now.

In conclusion, it seems that this code for SkipLists is almost ready for Deployment testing. The times are fast enough that we should be able to see gains in hard square or hard sphere simulations involving only 100's of pairwise actors.

Attachments:

SkipList-04-checked.nb