Over on stack exchange, someone asked something along the lines: is it possible to prove that Rule 110 outputs black cells with an average asymptotic density $4/7$? This question is now over $10$ years old, but a similar question came up again more recently. The purpose of this memo is to follow up on Peter Shor's suggestion extending a typical fixed point calculation to larger domain size.

For a radius $r$ let us reason about the probabilities for finding a sequence of $2r+1$ particular values, which can be integer encoded $n \in [0, 2^{2r+1}-1]$. Each $n$ is the image of a finite set of sequences of $2r+3$ particular values, which can be encoded as $\{x,y,z\} \in [0, 2^{2r+1}-1]^3$, assuming that $x$ and $y$ overlap on 2 values and similar for $y$ and $z$. For example with rule 110, $n=7$, we have the following valid triplets for $\{x,y,z\}$:

FromDigits[#, 2] & /@ Partition[#, 3, 1] & /@ Select[Tuples[{0, 1}, 5],
  FromDigits[CellularAutomaton[110, #][[2 ;; -2]], 2] == 7 &]

Out[] = {{1, 2, 5}, {1, 3, 6}, {2, 5, 2}, {2, 5, 3}, {3, 6, 5}, {5, 2, 5}, 
              {5, 3, 6}, {6, 5, 2}, {6, 5, 3}}

In this example, $P(7)$ can be calculated by summing over $P(x)P(y | x)P(z | y)$ for all the 9 triplets listed above. In general, this sets up the possibility of a fixed point iteration, with one added difficulty: it can happen that $P(n)=0$. Once the $P(n)$ are known, they directly determine $P(\text{black})$ and $P(\text{white})$. The code is not exactly a one-liner, but almost:

ConditionalProbability[zeroes_][list_
  ] := Module[{first, rest},
  If[! DisjointQ[zeroes, list], 0,
   first = p[First[list]];
   rest = Map[If[EvenQ[#],
       p[#]/(p[#] + p[# + 1]),
       p[#]/(p[#] + p[# - 1])
       ] &, Rest[list]];
   first*Apply[Times, rest]]]

DetailedDensityEstimate[rule_, rad_ : 1, cut_ : 2^(-10)
  ] := Module[{primitive, check, update, keys, zeroes, init, res},
  keys = Map[p, Range[0, 2^(2 (rad - 1) + 1) - 1]];
  primitive = GroupBy[Tuples[{1, 0}, 2 rad + 1],
    p[FromDigits[CellularAutomaton[rule, #][[2 ;; -2]], 2]] &];
  zeroes = Map[First, Select[keys, Lookup[primitive, #, True] &]];
  check = {};
  While[UnsameQ[check,
    update = Map[Total, Map[ConditionalProbability[zeroes][
         FromDigits[#, 2] & /@ Partition[#, 2 (rad - 1) + 1, 1]
         ] &, primitive, {2}]]],
   zeroes = 
    Union[zeroes, Map[First, Keys[Select[update, # == 0 &]]]];
   check = update];
  Map[Set[update[p[#]], 0] &, zeroes];
  update = KeySort[update];
  init = Map[# -> If[MemberQ[zeroes, First[#]], 0,
       N[1/(Length[keys] - Length[zeroes])]
       ] &, keys];
  res = FixedPoint[Function[{vals},
     KeyValueMap[#1 -> (#2 /. vals) &, update]], init,
    SameTest -> (EuclideanDistance[Last /@ #1, Last /@ #2] < cut &)];
  Map[Total, Map[Last, GroupBy[res,
     IntegerDigits[#, 2, 2 (rad - 1) + 1
          ][[rad]] & @@ First[#] &], {2}
    ]]
  ]

We simply map this function over increasing radius size to obtain increasingly accurate estimates of the density of white and black cells:

res = AbsoluteTiming[
     DetailedDensityEstimate[110, #]
     ] & /@ Range[6];
Total@*Values@*Last /@ res
Out[] = 1, 1, ...

ListLinePlot[MapIndexed[Callout[#1, First[#2] - 1] &,
  Transpose[Values@*Last /@ res]]]

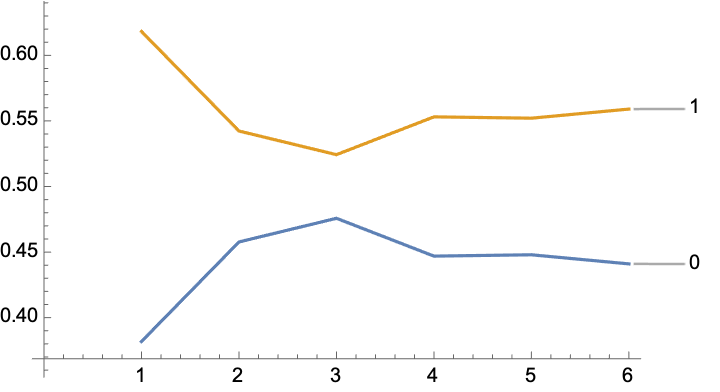
Unfortunately, this does not prove that the density of black cells approaches $4/7$. We could try to go to a larger radius, but as we do, times increase exponentially:

ListLogPlot[First /@ res]

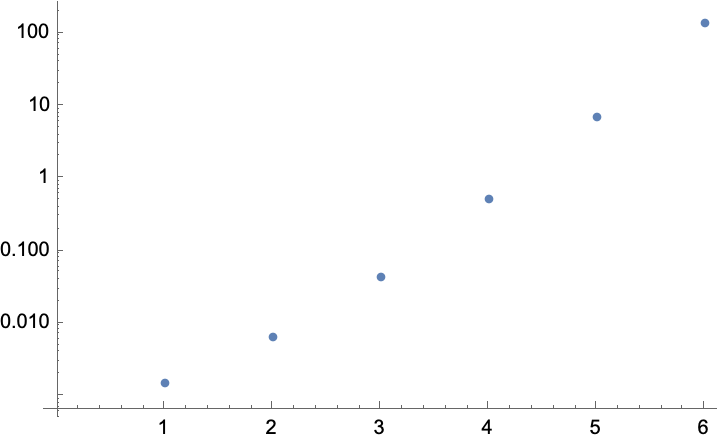
Although this analysis is a nice bit of mathematics, it falls short of proof. It's unknown to me whether a proof even exists. If we carefully examine how the fixed point equations become more complicated with increasing radius, it seems unlikely that this approach will lead to exact symbolic results such as the quoted $4/7$.