I use DSolve and NDSolve to solve a set of differential equations respectively, where NDSolve specifies an implicit Euler method, and subtract the results of both solutions to obtain the truncation error curve, maximum truncation error, and corresponding positions of the implicit Euler method.
The code is as follows:
tstart = 0;
tend = 0.08;
stepsize = 0.00006;
n = (tend - tstart)/stepsize;
(*DSolve*)
sol1 = DSolve[{l il'[t] == vl[t], c vc'[t] == ic[t],
ir[t] == -ic[t] + il[t], vl[t] == 24 - vc[t], vr[t] == vc[t],
vr[t] == r ir[t], il[0] == 0, vc[0] == 0}, {ir[t], il[t], ic[t],
vr[t], vl[t], vc[t]}, t];
il[t_] = il[t] /. sol1[[1]];
pars1 = {r -> 22, l -> 2 10^-1, c -> 1 10^-4};
a = Evaluate[il[t] /. pars1];
Dil = Table[a, {t, 0, 0.08, stepsize}, 1];
(*NDSolve*)
components1 = {vI == ll iL'[t] + vC[t],
vC'[t] == iL[t]/cc - vC[t]/(rr cc), vC[0] == 0, iL[0] == 0};
pars2 = {vI -> 24, rr -> 22, ll -> 2 10^-1, cc -> 1 10^-4};
sol2 = NDSolve[{components1} /. pars2, {iL}, {t, 0, .2},
StartingStepSize -> stepsize,
Method -> {"FixedStep", Method -> {"LinearlyImplicitEuler"}}];
a = Evaluate[iL[t] /. sol2[[1]]];
NDil = Table[a, {t, 0, 0.08, stepsize}, 1];
(*Calculation error*)
errort = Table[tstart + stepsize*i, {i, 0, n}];
ilerror = Table[0, {i, 0, n}];
For[k = 1, k < n + 1, k++,
ilerror[[k]] = Dil[[k, 1]] - NDil[[k, 1]];
];
p1 = Table[Transpose[{errort, ilerror}], 1];
ListLinePlot[p1, AxesLabel -> {"s", "il[t]/A"},
PlotLegends -> {"LinearlyImplicitEuler"}, PlotStyle -> {Red},
PlotRange -> All]
ilpeak = FindPeaks[Abs[ilerror]]
{{151, 0.00191949}}
From the operation results, we can see that the maximum truncation error of il at the 151st point is 0.001919.
The following image is an error estimate for the implicit Euler method seen in a book. 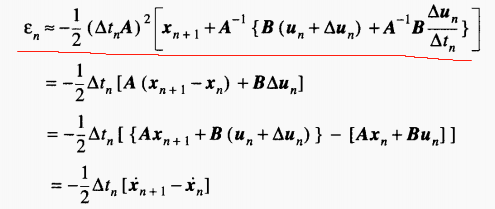
The calculation code for this method is as follows:
{r = 22, l = 2 10^-1, c = 1 10^-4, vi = 24, stepsize = 0.00006};
\[CapitalDelta]vi = 0;
A = {{0, -1/l}, {1/c, -1/(r c)}};
G = Inverse[A];
B = {1/l, 0};
Subscript[X, n + 1] =
Transpose[{{0.7909637667818027, 14.280468663134522}}];(*The il value of the 152nd position is calculated by DSolve*)
Error = Transpose[{{ilerror, vcerror}}];
Error = (-1/2*stepsize*stepsize*A . A) . (Subscript[X, n + 1] +
G . (B*(vi + \[CapitalDelta]vi) +
G . B*\[CapitalDelta]vi/stepsize))
{{0.000012766639933902838`}, {0.00028584581003691066`}}
The 0.000012766639933902838 in the calculation result is the il error calculated using the error estimation formula in the literature(ss shown in the picture).
The comparison shows that the results calculated by the two methods (0.001919... and 0.0000127...) differ greatly. What is the reason for this? Is it related to Mathematica's built-in algorithm?
The literature from which the formula is derived is shown in the attachment(p130 Equation (5.3.14))
 Attachments:
Attachments: