Yes, I can confirm that in this special case/example DiscretizeRegion[] does not work for some reason. But if it is done in a slightly different way (?) it does work:
(* points from your example: *)
pts = {{0.179783, 0.57135}, {0.279118, 0.609293}, {0.354784,
0.356823}, {0.402835, 0.0278031}, {0.512392, 0.235275}, {0.551364,
0.91872}, {0.606836, 0.924831}, {0.660189, 0.0157829}, {0.786429,
0.561368}, {0.961246, 0.585222}};
order = Most@Last@FindShortestTour[pts];
pts = pts[[order]];
(* perpendicular line for each side: *)
perpLines = PerpendicularBisector /@ Partition[Append[pts, First[pts]], 2, 1];
(* inner part of the lines - as region: *)
innerRegs = DiscretizeRegion[RegionIntersection[Polygon[pts], #]] & /@ perpLines;
(* ... and as a "chain of lines": *)
innerLines0 = MeshPrimitives[#, 1] & /@ innerRegs;
(* final result - assembling the "chain of lines": *)
innerLines = # //. {{x___, Line[{cc_, dd_}], m___, Line[{dd_, ee_}],
y___} :> {x, m, Line[{cc, ee}], y},
{x___, Line[{dd_, ee_}], m___, Line[{cc_, dd_}], y___} :> {x, m,
Line[{cc, ee}], y}} & /@ innerLines0;
(* ... and points where lines cross the polygon border: *)
ep = Flatten[innerLines /. Line[{p1_, p2_}] :> {p1, p2}, 2];
Graphics[{LightGreen, EdgeForm[Thick], Polygon[pts], PointSize[.03], Black, innerLines, Red, Point[ep]}]
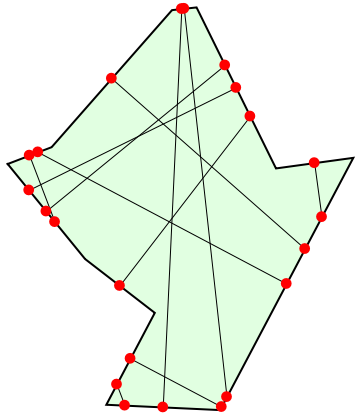
Hopefully this helps, and sorry for the late response! Regards --Henrik