I used these examples today when I taught the monotonicity of functions so that my students could better understand the concepts of increasing and decreasing functions. Both will appear in almost every section in a Calculus class and probably in other classes too, so you should be able to deal with them.
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus and was later generalized to the more abstract setting of order theory.
Definition of increasing functions
A function is called monotonically increasing (also increasing or non-decreasing) if for all $x$ and $y$ such that $x\leq y$ one has $f\left(x\right) \leq f\left(y\right)$, so $f$ preserves the order
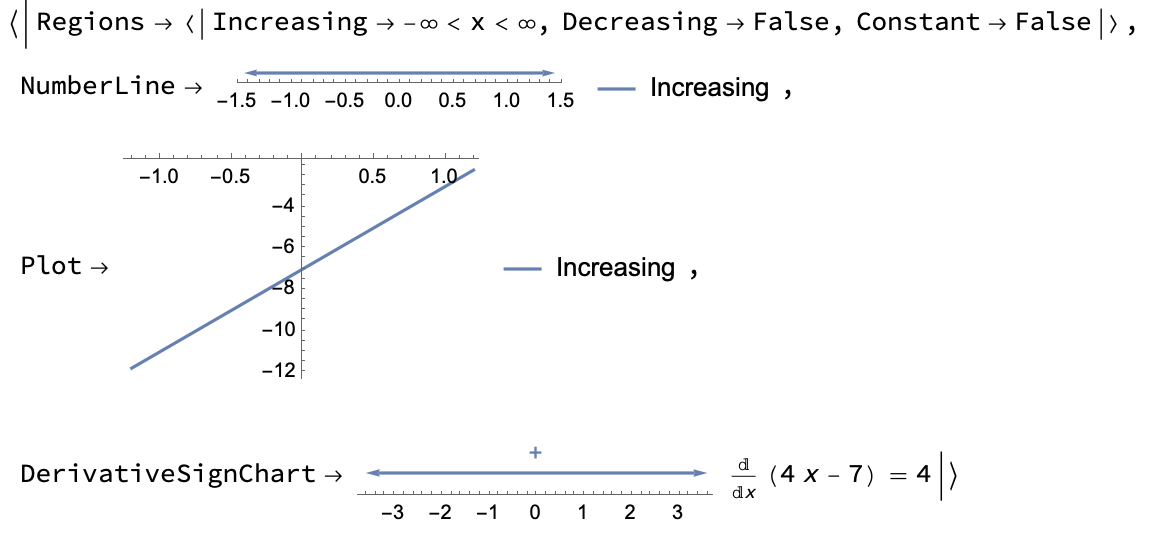
Examine the monotonicity of the function $$f(x)=4x-7$$ The domain of the function is $D_f=\mathbb{R}$.
Let $x_1,x_2 \in D_f $ and $x_1<x_2$, then we have:
$$\begin{align} x_1&<x_2 \\ 4x_1&<4x_2 \\ 4x_1-7&<4x_2-7 \\ f(x_1)&<f(x_2) \end{align}$$
Hence the function $f(x)$ is increasing on $D_f$
ResourceFunction["FunctionMonotonicity"][4 x - 7, x, All]
 - Example 2
- Example 2
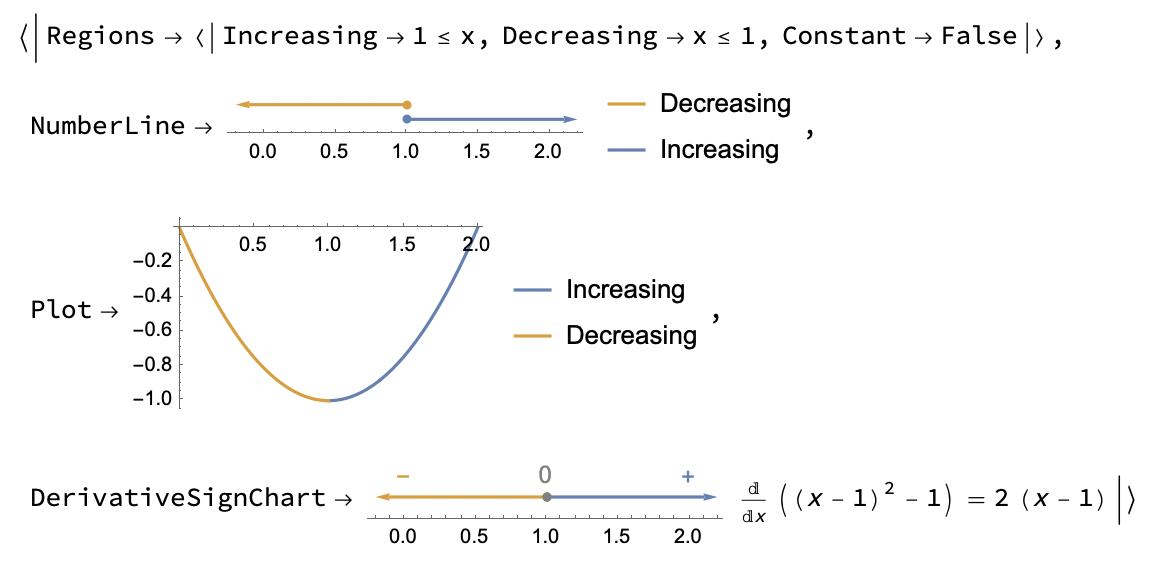
Examine the monotonicity of the function $$f(x)=(x-1)^2-1, \quad x> 1$$ The domain of the function is $D_f=(1,\infty]$
Let $x_1,x_2 \in D_f $ and $x_1<x_2$, then we have: $$\begin{align} x_1&<x_2 \Rightarrow \\ x_1-1&<x_2-1 \Rightarrow \\ (x_1-1)^2&<(x_2-1)^2 \Rightarrow \\ (x_1-1)^2-1&<(x_2-1)^2-1 \Rightarrow \\ f(x_1)&<f(x_2) \end{align}$$ Hence the function $f(x)$ is increasing on $D_f$
ResourceFunction["FunctionMonotonicity"][(x - 1)^2 - 1, x, All]
Definition of decreasing functions
A function is called monotonically decreasing (also decreasing or non-increasing) if, whenever $x\leq y$, then $f\left(x\right) \geq f\left(y\right)$, so it reverses the order
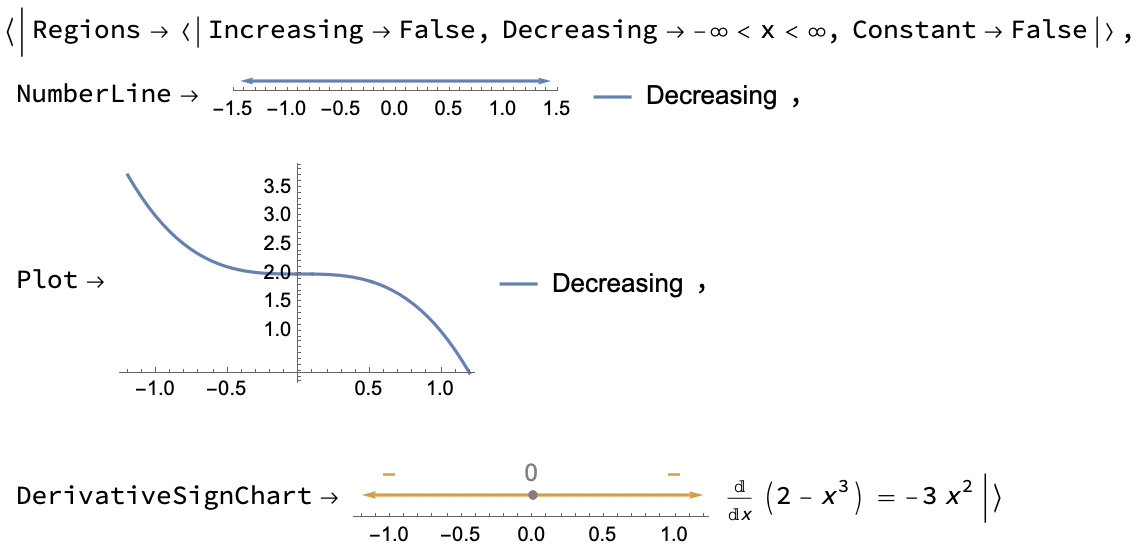
Examine the monotonicity of the function $$f(x)=2-x^3$$ The domain of the function is $D_f=\mathbb{R}$.
Let $x_1,x_2 \in D_f $ and $x_1<x_2$, then we have: $$\begin{align} x_1&<x_2 \Rightarrow \\ x_1^3&<x_2^3 \Rightarrow \\ -x_1^3&>-x_2^3 \Rightarrow \\ 2-x_1^3&>2-x_2^3 \Rightarrow \\ f(x_1)&>f(x_2) \end{align}$$ Hence the function $f(x)$ is decreasing on $D_f$
ResourceFunction["FunctionMonotonicity"][2 - x^3, x, All]