BooleanRegion seems to only deal with certain types of 3D regions. The following example works:

DiscretizeRegion[BooleanRegion[And, {Ball[{0, 0, 0}, 2], Ball[{3, 0, 0}, 2]}]]

This next example doesn't work:

c = 0.75; r = 89; R = 144; d = 2;
DiscretizeRegion[BooleanRegion[And, {ParametricPlot3D[{
 c (Cos[t] + d) Cos[u],
 c (Cos[t] + d) Sin[u],
 c Sin[t]
 }, {u, 0, 2 Pi}, {t, 0, 2 Pi}, Mesh -> False, 
PlotStyle -> Opacity[0.5], MaxRecursion -> 2], ParametricPlot3D[{
 c ((Cos[r t] + d) Cos[R t]) + u Cos[r t] Cos[R t],
 c ((Cos[r t] + d) Sin[R t]) + u Cos[r t] Sin[R t],
 -c (Sin[r t]) - u Sin[r t]
 }, {t, 0, 1/55 Pi}, {u, -0.08, 0.08}, MaxRecursion -> 0, 
Mesh -> False, PlotStyle -> Thickness[0.06], PlotPoints -> 50]}]]

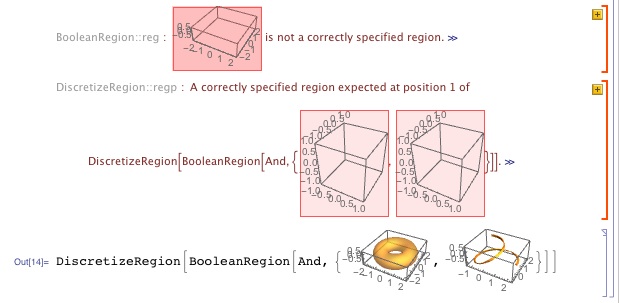
Perhaps it is treating the regions generated by ParametricPlot3D as hollow shells that are not filled in? Am I correct to assume that what I am generating here with ParametricPlot3D are technically "region"s? If so, they why is it that RegionUnion, RegionDifference, RegionIntersection, BooleanRegion, and DiscretizeRegion cannot handle them?

Basically what I'm looking for here is a way to add, subtract, and perform boolean operations on various 3D regions generated with ParametricPlot3D, for purposes of exporting to STL. So far, the only option has been "Show", but that only does region addition, not subtraction. Can any of the new geometric functions be used for my purposes? So far, it seems the answer is "no". Please forgive me if I have overlooked something simple.

I'd also like to echo this post. What is the point of DiscretizeRegion or TriangulateMesh if you can't export it to STL? For instance, I want export a Graphics3D Tube around a bezier/ bspline curve to STL, but I get this error: Export::type: MeshRegion cannot be exported to the STL format. >>