For the new school year, Wolfram|Alpha is providing an assortment of improvements for our Step-by-Step formula functionality. One element is expanded steps to provide better context and physical understanding for a wide range of formulas in the domains of Physics and Earth Science. These include expanded introductions for specific formulas, illustrative schematics, and the first derivations of formulas from the basic principles.

Extended Definitions

By default Wolfram|Alpha introduces a formula in its Step-by-Step functionality by stating the variables that that the formula relates. We are currently expanding on this to give more information on the usage and purpose of those variables as well as some of the context and restrictions on that particular formula.

Sometimes this is just as simple of explaining the formula, for example with determining average speed: But it can also convey many of the assumptions used in these formulas such as holding variables constant or with other restrictions. Here is equation of motion involving speed, distance and time: This new feature also highlights that certain formulas such as many earth science formulas are empirical and thus their formulas are structured to fit the data, rather than relying on fundamental principles. For example earthquake fault slip calculations: 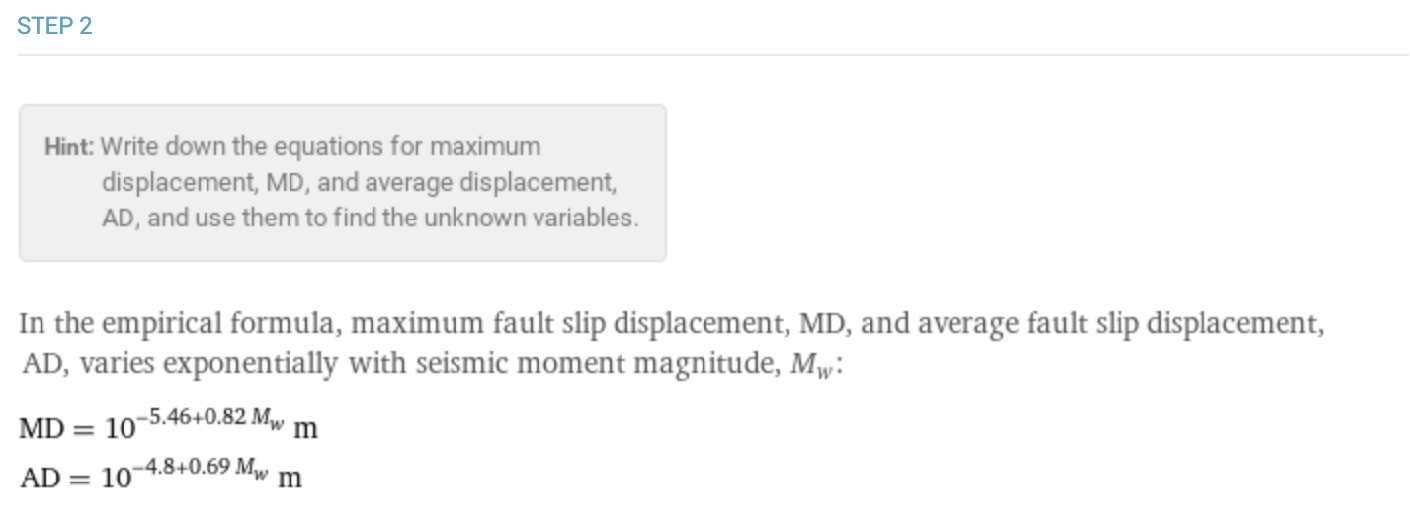These descriptions can work together to make more complicated calculations clearer. For example the formula for mechanical power using work and time is described: 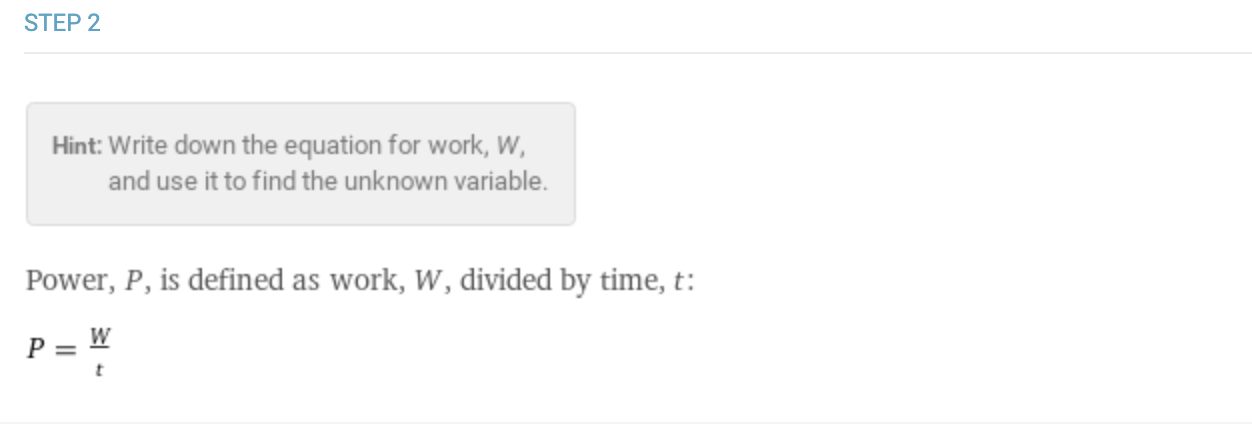But if we look at the calculation using force and speed, Wolfram|Alpha describes how this equation was derived: At their most complex, these extended definitions can describe the specific problem and assumptions in more detail and how this solution is arrived at. For example the probability of exceedance formula's description highlights several assumptions inherent to the formula:

Schematics

A picture is worth a thousand words. Referencing an image helps when describing the parameters of a physical system. The first set of Step-by-Step formula schematics are now available on Wolfram|Alpha.

These schematics make it easier to identify the variables and visualize the motion for calculations like centripetal acceleration where the direction of of the acceleration and the instantaneous velocity can be non-intuitive: This can also be the case when considering angular velocity for centripetal acceleration:

Derivations

In many cases the deriving the formula itself is the point of the exercise. To this end, Wolfram|Alpha is including derivations for common mechanics formulas beginning with projectile motion and the equations for a pendulum subject to small oscillations.

Wolfram|Alpha provides Step-by-Step instructions for deriving these formulas using basic concepts in physics such as conservation of energy, balance of forces and the one dimensional kinematic equations.

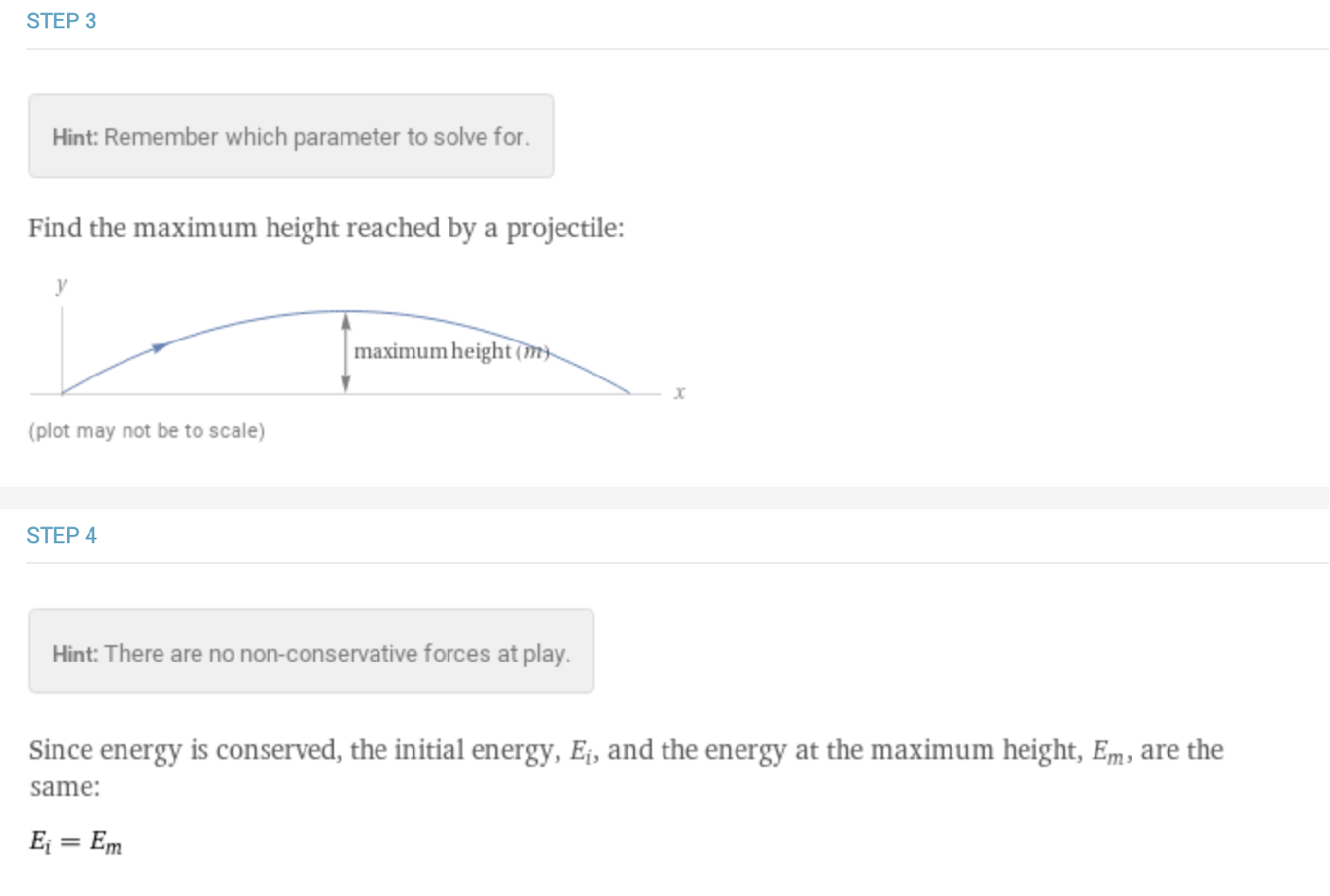
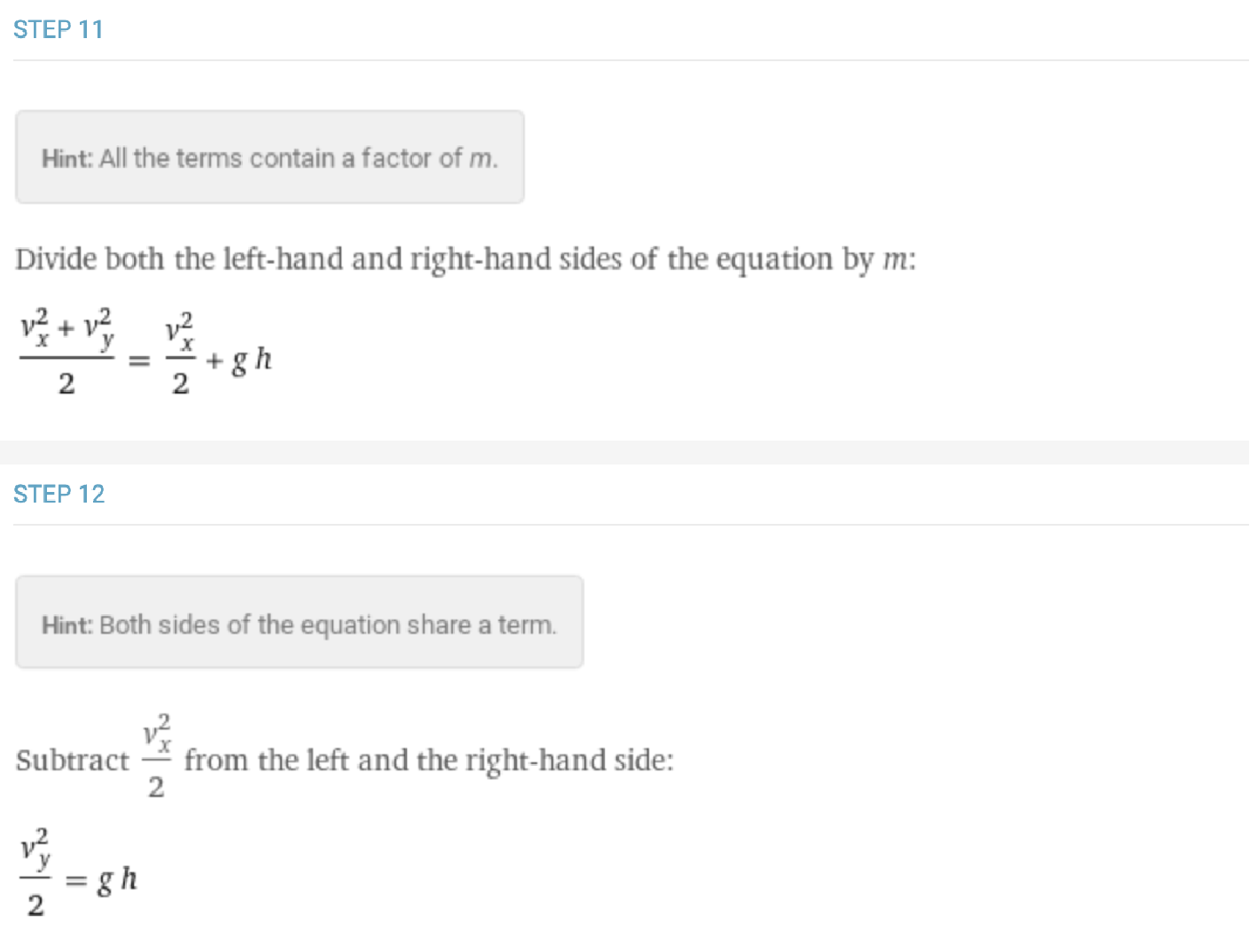
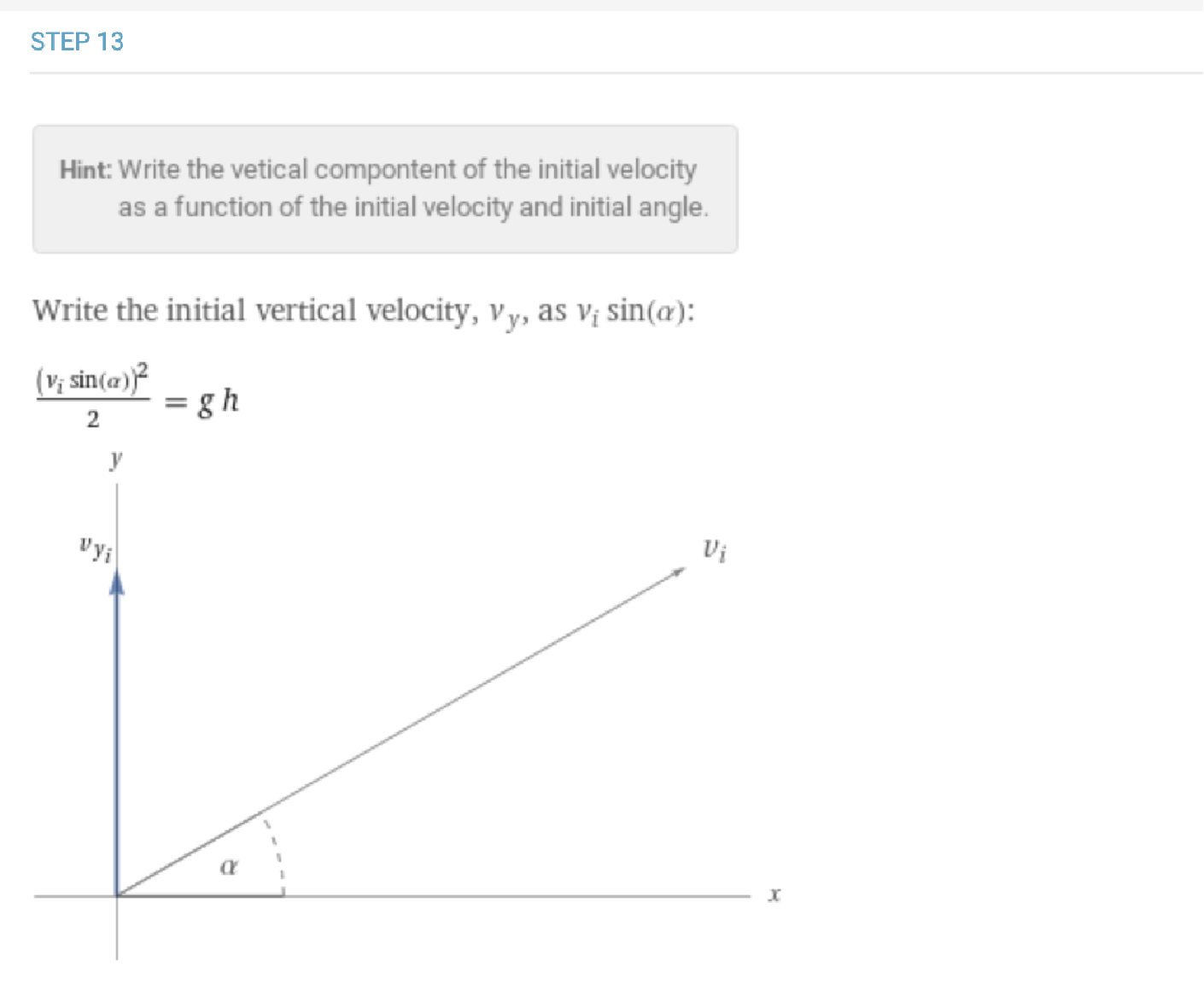
The projectile motion derivations guide the user through the process of determining maximum height, travel time and horizontal distance travelled. In the case of maximum height, these steps focus on the conservation of energy to show how kinetic energy becomes gravitational potential energy and thus can be used to find the maximum height. 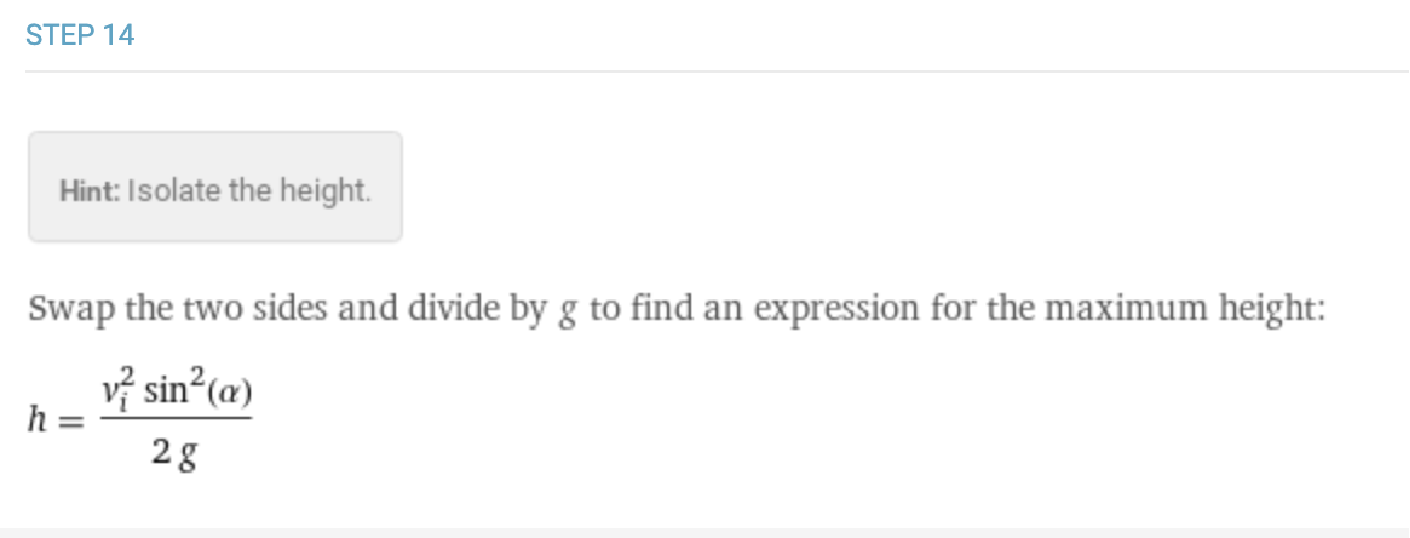For the small oscillation case of a pendulum, Wolfram|Alpha provides derivations for the equations for period, frequency and maximum speed of the bob, or the weight at the end of the pendulum. For example, when working through the steps for the period, Wolfram|Alpha begins with the determining the net forces before comparing the form of the calculation to that of a simple harmonic oscillator.

Conclusion

This is just the first taste of the material that on the way. Later this year we will have similar support in terms of schematics and descriptions for formulas in the areas of Electricity & Magnetism, Statistical Physics and Thermodynamics as well as more derivations for Mechanics.

Also follow these links to learn more about our expanded formula coverage and improvements to unit conversions.