I am trying to determine the poles of a function, which can be simplified to finding the poles of a function using Wolfram alpha in the following way:

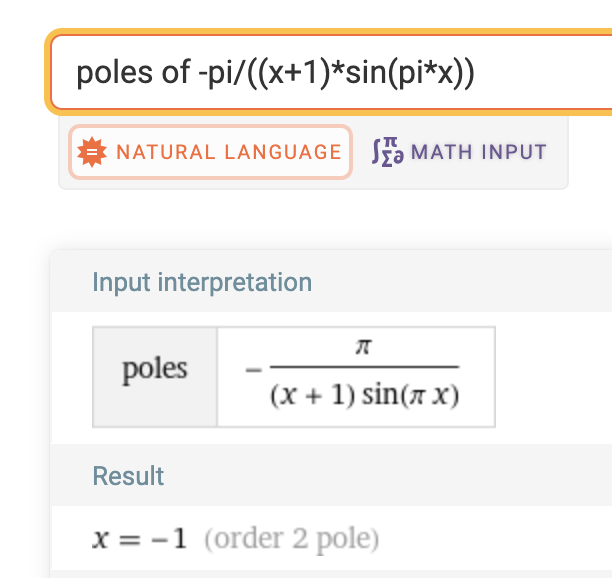
In this case, I am certain that there should be simple poles at all integer values (except -1). For example, 1/sin(pi x) alone has poles at all integer values. Furthermore, at x=-2 we can expand the function in the following way

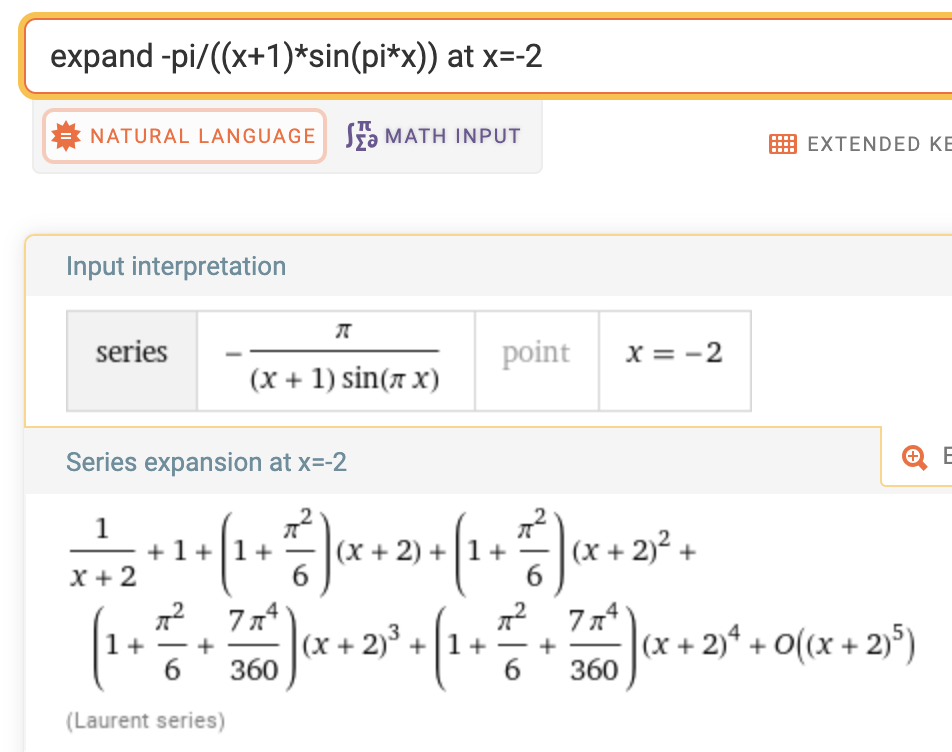
which suggests a simple pole at -2 with residue 1.

Is mathematica only returning the higher-order poles (I checked other simple cases and it returns them all)? Does the program perhaps not always check all values where the denominator is zero and so maybe doesn't return all poles? Or am I simply wrong about something?

PS: I had done these calcs in Mathematica previously but my work license has expired and now I cannot double-check the results I had there.