Is not the answer.
If your integral is from {k,-Infinity,Infinty} we can use a FourierTransform to compute integral.
ClearAll["`*"]; Remove["`*"]
F[k_] := 1/Sqrt[\[Pi] a] Sin[k a]/k;
FourierTransform[F[k] Exp[I (k x - (\[HBar] k^2)/(2 m) t)]*Exp[-I k x] // Expand, k, x] // Simplify
(*((1/4 + I/4) t^(3/2) \[HBar]^(
3/2) (Erfi[((1/2 + I/2) Sqrt[m] (a - x))/(Sqrt[t] Sqrt[\[HBar]])] +
Erfi[((1/2 + I/2) Sqrt[m] (a + x))/(
Sqrt[t] Sqrt[\[HBar]])]))/(Sqrt[a] m^(3/2) ((I t \[HBar])/m)^(3/2)
)*)
then:
Clear[Psiappx2];
a = 1;
m = 1;
\[HBar] = 1;
Psiappx2[x_, t_] := ((1/4 + I/4) t^(3/2) \[HBar]^(
3/2) (Erfi[((1/2 + I/2) Sqrt[m] (a - x))/(Sqrt[t] Sqrt[\[HBar]])] +
Erfi[((1/2 + I/2) Sqrt[m] (a + x))/(Sqrt[t] Sqrt[\[HBar]])]))/(
Sqrt[a] m^(3/2) ((I t \[HBar])/m)^(3/2));
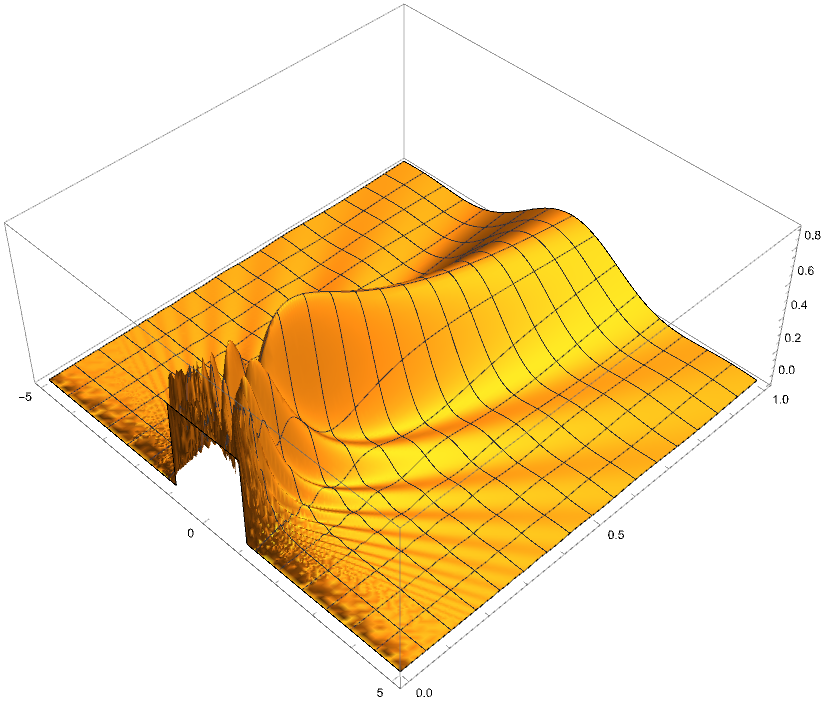
Plot3D[Abs[Psiappx2[x, t]]^2, {x, -5, 5}, {t, 0, 1}, PlotRange -> All,PlotPoints -> 100]