An axes aligned bounding box (AABB) tree, a type of bounding volume hierarchy, is a spatial data structure designed to efficiently find overlapping bounding boxes. It is often used to find broad-level collisions in applications such as collision detection and ray tracing.
Question
I have an implementation in WL that uses some Compile and DataStructure, but is mostly top-level WL code. I'm looking to increase performance, while staying in the WL ecosystem.
Are there any tips to speed up my code? In particular any tips to port this over to compiled code using FunctionCompile & friends? Side note, would be nice if this was a builtin DataStructure :)
I've posted the code below. Feel free to ask any questions about how it works, etc.
Examples
Basic example
Bounding boxes are of the form $\{\{x_{min}, x_{max}\}, \{y_{min}, y_{max}\}, \{z_{min}, z_{max}\}\}$.
Let's create the AABB tree over 3 bounding boxes and make 1 query bounding box:
bboxes = {
{{0, 1}, {0, 1}, {0, 1}},
{{0.5, 1.5}, {0.25, 1.5}, {0.3, 0.7}},
{{0.7, 0.8}, {0.8, 2}, {0.2, 0.8}}
};
testbbox = {{0.6, 0.9}, {1.1, 1.4}, {0.6, 0.9}};
Create the data structure:
aabbtree = AABBTree[bboxes];
Find the indices of the bounding boxes that overlap testbbox:
overlaps = OverlappingBBoxes[aabbtree, testbbox]
(* {2, 3} *)
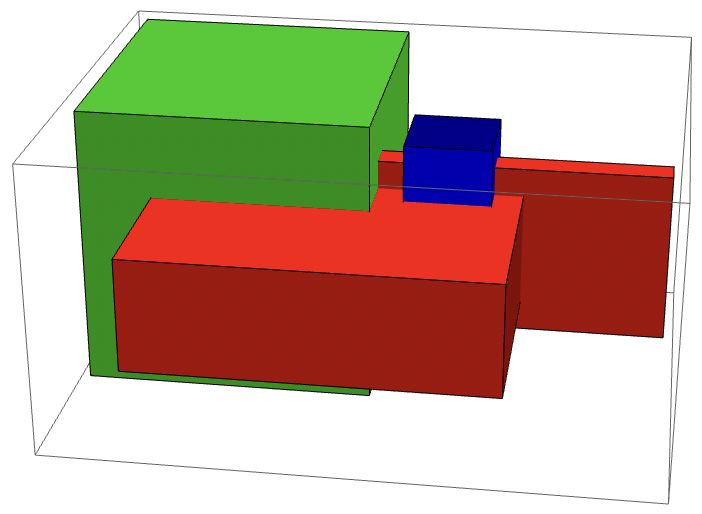
Visualize (query box in blue, overlapping in red, disjoint in green):
Graphics3D[{
{FaceForm[Green], Cuboid @@@ Transpose[Delete[bboxes, Partition[overlaps, 1]], {1, 3, 2}]},
{FaceForm[Red], Cuboid @@@ Transpose[bboxes[[overlaps]], {1, 3, 2}]},
{Blue, Cuboid @@ Transpose[testbbox]}
}]
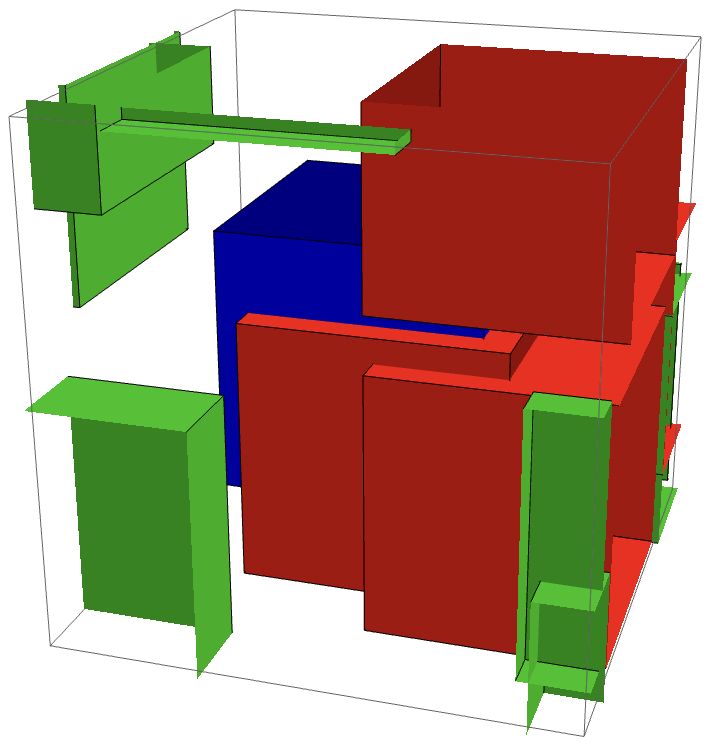
4000 bounding boxes, 1 query
randomBBox[n_] :=
With[{llcorners = RandomReal[{-10, 10}, {n, 3}]},
Transpose[{llcorners, llcorners + RandomReal[{1, 1}, {n, 3}]}, {3, 1, 2}]
]
SeedRandom[1];
bboxes = randomBBox[4000];
testbbox = randomBBox[1][[1]];
aabbtree = AABBTree[bboxes]; // AbsoluteTiming
(* {0.018875, Null} *)
(overlaps = OverlappingBBoxes[aabbtree, testbbox]) // AbsoluteTiming
(* {0.000692, {1817, 3935, 878, 87}} *)
Graphics3D[Cuboid @@@ Transpose[bboxes, {1, 3, 2}]]

Graphics3D[{
{FaceForm[Green], Cuboid @@@ Transpose[Delete[bboxes, Partition[overlaps, 1]], {1, 3, 2}]},
{FaceForm[Red], Cuboid @@@ Transpose[bboxes[[overlaps]], {1, 3, 2}]},
{Blue, Cuboid @@ Transpose[testbbox]}},
PlotRange -> testbbox,
PlotRangePadding -> Scaled[0.25]
]
100000 bounding boxes, 100000 queries
SeedRandom[1];
bboxes = randomBBox[100000];
testbboxes = randomBBox[100000];
aabbtree = AABBTree[bboxes]; // AbsoluteTiming
(* {0.235465, Null} *)
OverlappingBBoxes[aabbtree, testbboxes[[1]]]; // AbsoluteTiming
(* {0.001988, Null} *)
I suspect this can be sped up substantially:
Scan[OverlappingBBoxes[aabbtree, #]&, testbboxes]; // AbsoluteTiming
(* {44.8445, Null} *)
Code
AABBTree[bboxes_] :=
Block[{$RecursionLimit = ∞},
iAABBTree[1, MapIndexed[Join, Flatten /@ bboxes][[Ordering[bboxes[[All, 1, 1]]]]]]
]
iAABBTree[d_, bboxestagged_] :=
Block[{len, n, x, Sleft, Scent, Sright, node},
len = Length[bboxestagged];
If[len <= 16, Return[centerNode3D[d, Null, bboxestagged]]];
n = Ordering[bboxestagged[[All, 2d-1]], {Quotient[len+1, 2]}][[1]];
x = Mean[bboxestagged[[n, 2d-1 ;; 2d]]];
{Sleft, Scent, Sright} = partitionIntervals3D[d, bboxestagged, x];
node = centerNode3D[d, x, Scent];
If[Length[Sleft] > 0, node["SetLeft", iAABBTree[Mod[d+1, 3, 1], Sleft]];];
If[Length[Sright] > 0, node["SetRight", iAABBTree[Mod[d+1, 3, 1], Sright]];];
node
]
centerNode3D[d_, x_, {}] := CreateDataStructure["BinaryTree", {x, {}, {}, {}, {}, {}, {}, {}, -$MaxMachineNumber, $MaxMachineNumber, d}]
(* {center ordinate, xmins, ymins, zmins, xmaxs, ymaxs, zmaxs, inds, dmin, dmax, d} *)
(* xmins are the xmin values of all bboxes in this node, ymins, etc follow suit *)
(* inds are the respective indices of the bboxes in this node *)
(* dmin & dmax are the bounds of all bounding boxes in dimension d (the splitting dimension) *)
centerNode3D[d_, x_, intstagged_] :=
CreateDataStructure["BinaryTree",
{
x,
#1, #2,
#3, #4,
#5, #6,
Developer`ToPackedArray[#7, Integer],
Switch[d, 1, #1[[1]], 2, Min[#3], 3, Min[#5]], Max[Switch[d, 1, #2, 2, #4, 3, #6]],
d
}& @@ Transpose[intstagged]
]
partitionIntervals3D[d_, intstagged_, x_] :=
Block[{data, spec},
data = Partition[partitionIntervals3DC[d, intstagged, x], 7];
spec = Round[data[[-1]]];
{data[[1 ;; spec[[1]]]], data[[spec[[1]]+1 ;; spec[[2]]]], data[[spec[[2]]+1 ;; -2]]}
]
partitionIntervals3DC = Compile[{{d, _Integer}, {intstagged, _Real, 2}, {x, _Real}},
Block[{mnp, mxp, cright = 0., ccenter = 0., bagright = Internal`Bag[Most[{0.}]], bagcenter = Internal`Bag[Most[{0.}]], bagleft = Internal`Bag[Most[{0.}]]},
mnp = 2d-1;
mxp = mnp+1;
Do[
If[Compile`GetElement[i, mxp] < x,
Internal`StuffBag[bagright, i, 1];
cright++,
If[Compile`GetElement[i, mnp] > x,
Internal`StuffBag[bagleft, i, 1],
Internal`StuffBag[bagcenter, i, 1];
ccenter++
]
],
{i, intstagged}
];
Join[Internal`BagPart[bagright, All], Internal`BagPart[bagcenter, All], Internal`BagPart[bagleft, All], {cright, cright + ccenter, 0., 0., 0., 0., 0.}]
],
CompilationTarget -> "C",
RuntimeOptions -> "Speed"
];
OverlappingBBoxes[tree_?DataStructureQ, bbox:{{x1_, x2_}, {y1_, y2_}, {z1_, z2_}}] :=
Block[{bag, stack, node, a, b, d1, d2, d3, d4, d5, d6, d7, d8, d9, d10, d11},
bag = Internal`Bag[];
stack = CreateDataStructure["Stack"];
stack["Push", tree];
While[!stack["EmptyQ"],
node = stack["Pop"];
{d1, d2, d3, d4, d5, d6, d7, d8, d9, d10, d11} = node["Data"];
{a, b} = bbox[[d11]];
If[Length[d2] > 0 && (d9 <= a <= d10 || d9 <= b <= d10 || a <= d9 <= d10 <= b),
Internal`StuffBag[bag, Pick[d8, bboxOverlaps[d2, d3, d4, d5, d6, d7, x1, x2, y1, y2, z1, z2], 1], 1];
];
If[d1 =!= Null,
If[a < d1 && !node["LeftNullQ"], stack["Push", node["Left"]]];
If[d1 < b && !node["RightNullQ"], stack["Push", node["Right"]]];
];
];
Internal`BagPart[bag, All]
]
bboxOverlaps = Compile[{{epx1, _Real}, {epx2, _Real}, {epy1, _Real}, {epy2, _Real}, {epz1, _Real}, {epz2, _Real}, {x1, _Real}, {x2, _Real}, {y1, _Real}, {y2, _Real}, {z1, _Real}, {z2, _Real}},
Boole @ And[
epx1 <= x1 <= epx2 || epx1 <= x2 <= epx2 || (x1 <= epx1 <= epx2 <= x2),
epy1 <= y1 <= epy2 || epy1 <= y2 <= epy2 || (y1 <= epy1 <= epy2 <= y2),
epz1 <= z1 <= epz2 || epz1 <= z2 <= epz2 || (z1 <= epz1 <= epz2 <= z2)
],
CompilationTarget -> "C",
Parallelization -> True,
RuntimeOptions -> "Speed",
RuntimeAttributes -> {Listable}
];