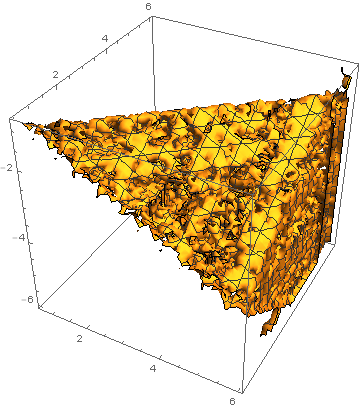
One wants to use Boole] and bring the functions from this old post [Re: Fläche sich überlagernder Objekte into 3D to new life.
An overkill
Graphics3D[
Table[If[Boole[ x/2 + (3 y)/5 + (5 z)/6 > 0 && -(x/2) + (3 y)/5 + (5 z)/6 < -(2/3) &&
x/2 - (3 y)/5 + (5 z)/6 < -(1/2) && x/2 + (3 y)/5 - (5 z)/6 > -(1/2)] == 1, Sphere[{x, y, z}]],
{x,0, 6, 0.2}, {y, -6, 6, 0.2}, {z, -6, 6, 0.2}]]
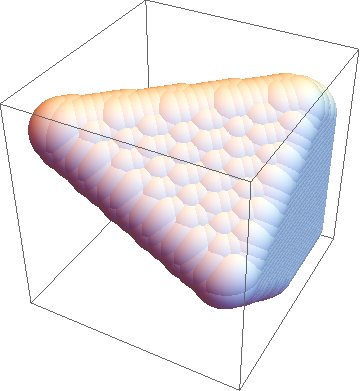
and obviously confused by the many (useless) inner points
ListSurfacePlot3D[
DeleteMissing[
Flatten[Table[
If[Boole[x/2 + (3 y)/5 + (5 z)/6 > 0 && -(x/2) + (3 y)/5 + (5 z)/6 < -(2/3) &&
x/2 - (3 y)/5 + (5 z)/6 < -(1/2) && x/2 + (3 y)/5 - (5 z)/6 > -(1/2)] == 1, {x, y, z},
Missing[]], {x, 0, 6, 0.1}, {y, -6, 6, 0.1}, {z, -6, 6, 0.1}],
2]], MaxPlotPoints -> 50]