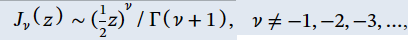from digital library of mathematical functions

First attempt:

Limit[BesselJ[v, z] Gamma[v + 1]/(1/2 z)^v, z -> 0, 
 GenerateConditions -> True]

Output : 1

That is, regardless the domain of v, the asymptotic equivalence holds.

I checked the following:

Limit[BesselJ[-3, z] Gamma[-3 + 1]/(1/2 z)^-3, z -> 0]

Output : ComplexInfinity

Next i tried the assumption:

Assuming[v \[Element] NegativeIntegers, 
 Limit[BesselJ[v, z] Gamma[v + 1]/(1/2 z)^v, z -> 0]]

Output : Indeterminate

Finally, i tried the correct :

Assuming[v \[NotElement] NegativeIntegers, 
 Limit[BesselJ[v, z] Gamma[v + 1]/(1/2 z)^v, z -> 0]]

Output : 1

Why is this happening?