Consider an objective function

v = ((i + lambda) Uem - (-1 + e) Uun)/(i (1 - e + i + lambda))

where

n = 1; beta = 0.6; W = 60; i=0.05;
L = (w/(beta (a e)^beta))^(1/(beta - 1));
lambda = ((1 - e) n L)/(1 - e n L);
Uem = w - 1/(w (1 - e));
b[e_] := b /. Solve[a W (1 + i)^(1/(1 - e) + 1/lambda - 1)- b \!\(\*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(\*FractionBox[\(1\), \(lambda\)] - 1\)]\(\((1 + i)\)^j\)\) == b + a W, b][[1]];
Uun = b[e] - 1/b[e];

under the conditions of $0\leq e \leq 1$ and $U_{em} > U_{un}$.

I would like to do some plotting by taking the following steps.

Step 1: Find e that maximizes v which will be yielded as a function of w with the parameter a, i.e., $e = f(w; a)$.

Step 2: Find e and w as the solution of $\frac{\partial f}{\partial w}=\frac{e}{w}$ for varying values of a $\in [0,1]$.

Step 3: Plot e and w obtained in Step 2 against a $\in [0,1]$.

My entire code for this is:

Clear["Global`*"];
n = 1; beta = 0.6; W = 60;
L = (w/(beta (a e)^beta))^(1/(beta - 1));
lambda = ((1 - e) n L)/(1 - e n L);
Uem = w - 1/(w (1 - e));
b[e_] := b /. Solve[a^2 W (1 + i)^(1/(1 - e) + 1/lambda -1) - b \!\(\*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(\*FractionBox[\(1\), \(lambda\)] - 1\)]\(\((1 + i)\)^j\)\) ==b + a^2 W, b][[1]];
Uun = b[e] - 1/b[e];
v = ((i + lambda) Uem - (-1 + e) Uun)/(i (1 - e + i + lambda));
f[e_, w_, a_, i_] = ArgMax[{v, e >= 0, e <= 1, Uem > Uun}, e];
With[{i = 5/100}, sol[a_] := sol[a] = FindRoot[D[f[e, w, a, i], w] == e/w, {{e, 0.5}, {w, 0.5}}]; {estar[a_], wstar[a_]} := {e /. sol[a], w /. sol[a]}; estarplot = Plot[estar[a], {a, 0, 1}, AxesLabel -> {s, SuperStar[\[CurlyEpsilon]]}, PlotRange -> {{0, 1}, {0, 1}}]; wstarplot = Plot[wstar[a], {a, 0, 1}, AxesLabel -> {s, SuperStar[w]}, PlotRange -> {{0, 1}, {0, 10}}];]
e = estarplot;
w = wstarplot;
Style[Row[{e, w}], ImageSizeMultipliers -> {0.6, 0.6}]

And I get empty graphs along with a list of error messages as follows.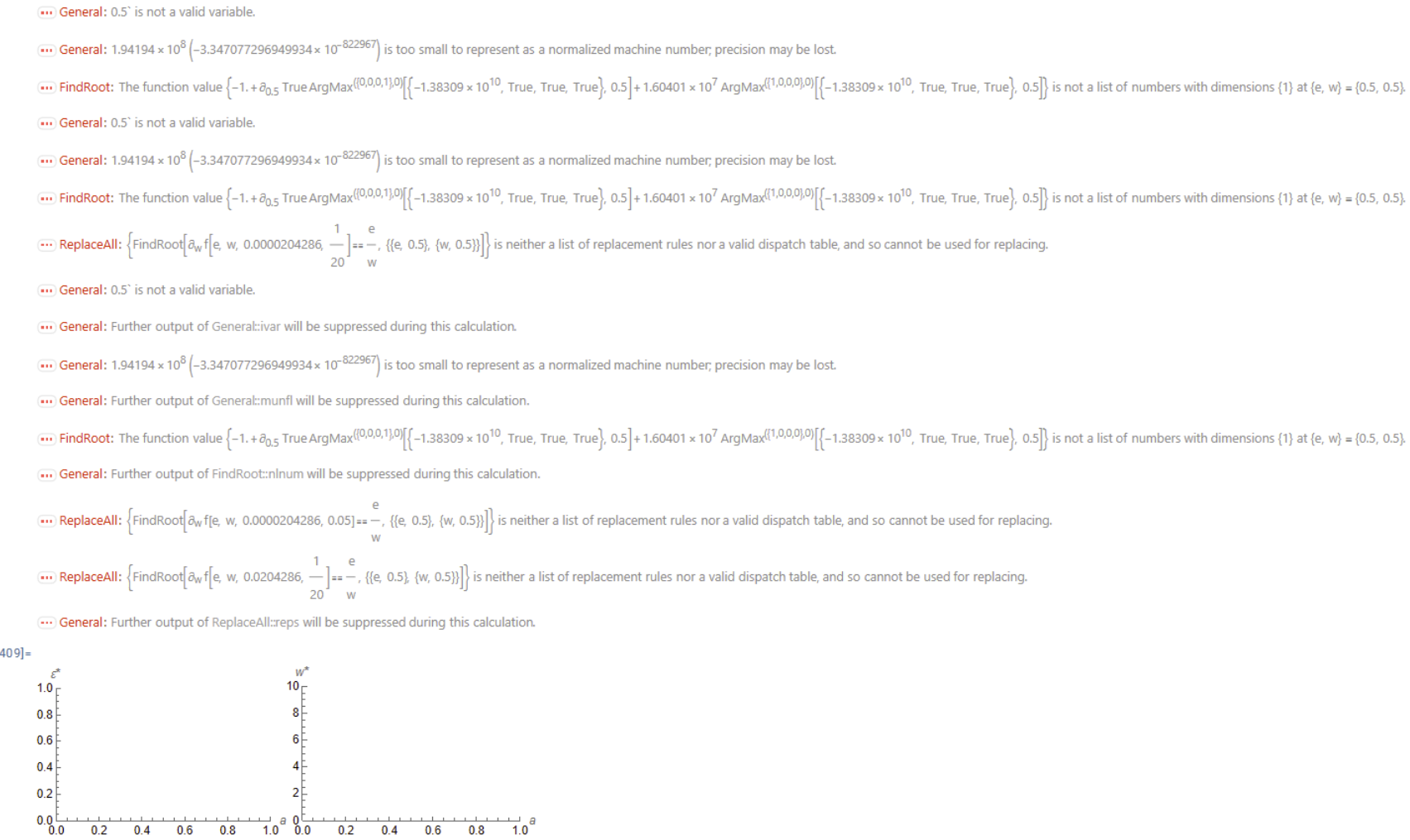

I also tried

f[e0_?NumericQ, a0_?NumericQ, w0_?NumericQ, i0_?NumericQ] := Block[{e = e0, a = a0, w = w0, i = i0}, ArgMax[{v, e >= 0, e <= 1, Uem > Uun}, e]];

in place of

f[e_, w_, a_, i_] = ArgMax[{v, e >= 0, e <= 1, Uem > Uun}, e];

but the result is the same. Can anyone help please?