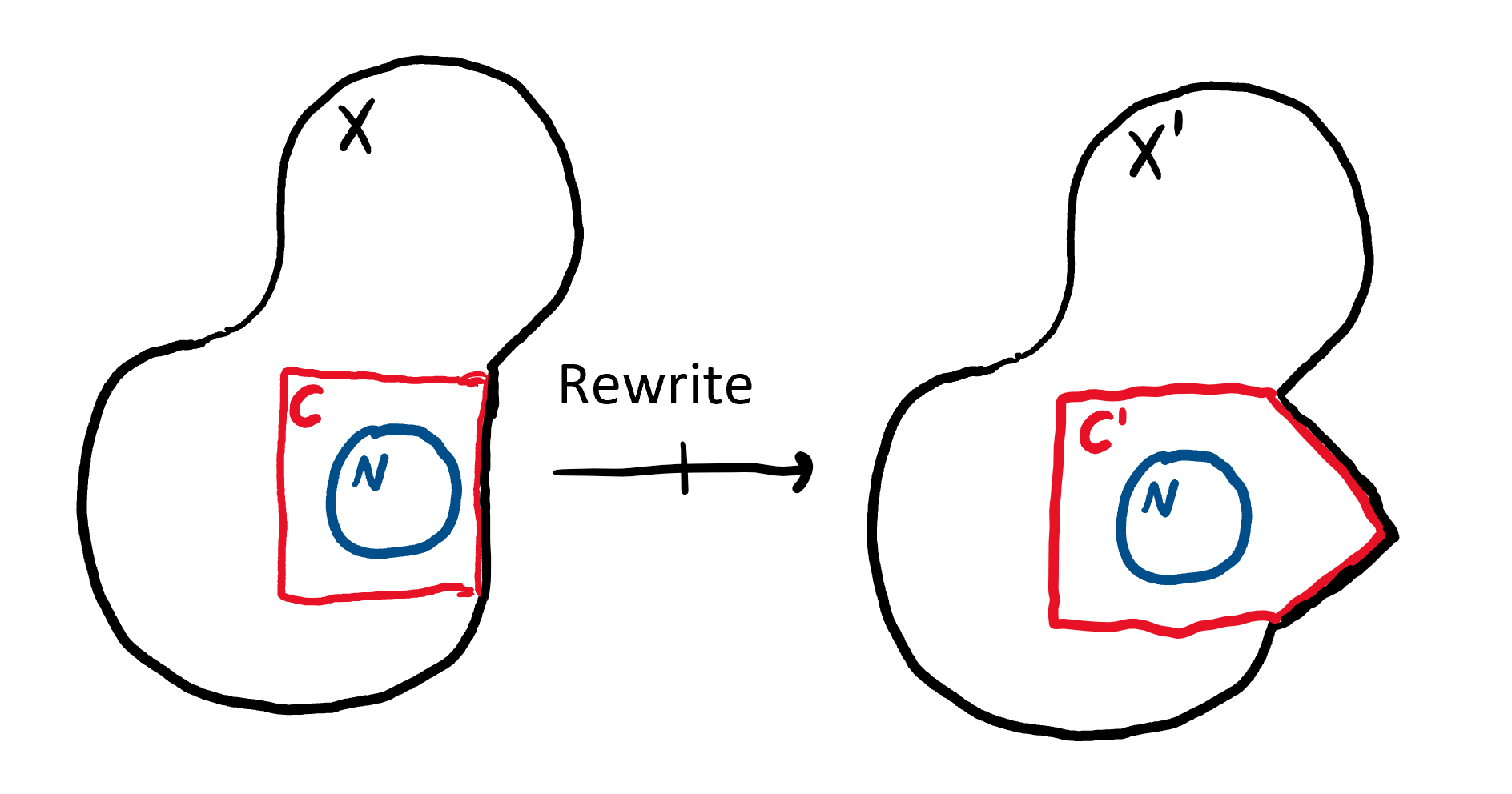
Goal: model multiway rewrite systems as a structured virtual double category ${\text{DPO}}(\mathbb C)$.
${\text{DPO}}(\mathbb C):{\text{vdc}}$ models composites of paths of rewrites and how they interact with ordinary morphisms in a given category $\mathbb C:{\mathbb C\text{at}}$. Modeling ${\text{DPO}}(\mathbb C)$ as a virtual double category would allow us to inherit categorical properties from other, related virtual double categories. We seek to define a representative ${\text{DPO}}$ so that ${\text{DPO}}(\mathbb C)\cong\mathbb C^{\text{DPO}} : {\text{vdc}}$. This representation makes it clear that ${\text{DPO}}:{\text{vdc}}$ was a choice, which opens the possibility of changing that choice.
DPO as a Virtual Double Category
Consider an ordinary category $\mathbb C$. Rewrites can be thought of as double pushout diagrams: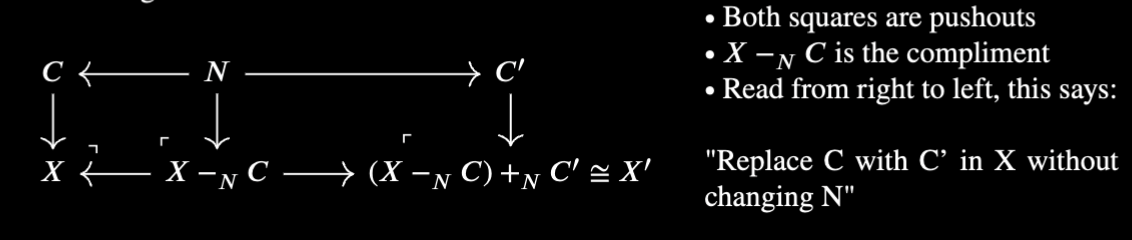 
Note we said nothing about the underlying category $\mathbb C$. One may think we would need to specify that $\mathbb C$ has pushouts and compliments. Abstractly, this does not matter. A DPO will only exist in a given category when the correct pushouts and compliments exist. If there are no pushouts, there will be no DPOs, if there are only certain pushouts, there will be only certain DPOs. If we want to generate DPOs from only the top portion of the diagram above (known as a rewrite rule), we would need certain pushouts/complements in $\mathbb C$.
To see this fact more clearly, we can define the above diagram as a structured functor from an abstract diagram that represents a DPO. Let $\to$ be the category with one morphism, so that $C^\to$ is the category whose objects are morphisms, and whose morphisms are commutative squares. For any category one can mark some of its morphisms. Namely, one can mark the pushouts of $\mathbb C^\to$ or one can mark the compliments of $\mathbb C^\to$, thus, for any category $\mathbb C^\to$ is in a sense bimarked, and its structure can be presented by a triple $(\mathbb C^\to, \text{comp, cart})$. There is another bimarked category $$\overset{L}\leftarrow\overset{R}\to \;= ({\text{Span}}, L, R) = \{\bullet\overset{L}\leftarrow\bullet\overset{R}\to\bullet\}$$
A marking preserving functor $\overset{L}\leftarrow\overset{R}\to \to (\mathbb C^\to, \text{comp, cart})$ is then a double pushout: it sends the left arrow to a compliment square, and the right arrow to a pushout square.
In this sense, $\text{DPO}(\mathbb C)_0 = \mathbb C\text{at}_\text{marked}(\overset{L}\leftarrow\overset{R}\to,\mathbb C^\to_\text{comp, cart} ) \sim (\mathbb C^\to)^{\leftarrow\to}:{\mathbb C\text{at}}$ is the Category of ${\text{DPO}}$ rewrites. We will see this is not enough to compose paths of rewrites.
We can abstract away from details of pushouts and compliments when discussing DPOs by writing them simply as an edges in some graph $X \overset{R}{\rlap{+}{\to}} X'$
We compose rewrites $X \overset{R_1}{\rlap{+}{\to}} X'\overset{R_2}{\rlap{+}{\to}} X''$ in $\mathbb C$ by taking pullbacks:
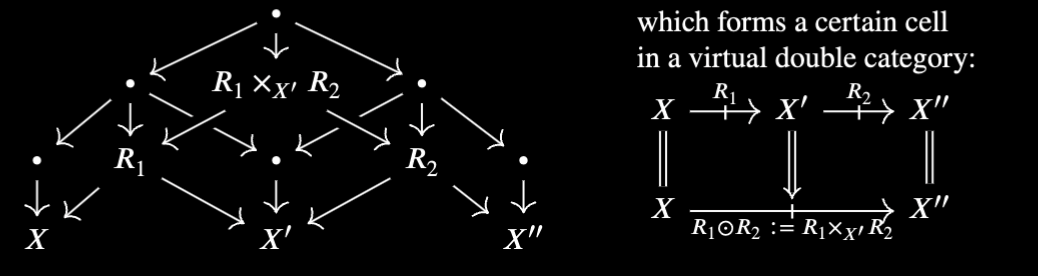
Note In order to compose we need the above pullbacks to exist in $\mathbb C$ and that pullback must result in a DPO. This is guaranteed to happen in an Adhesive category. However, we did not assume anything about $\mathbb C$. However, this is okay; if certain pullbacks do not exist in $\mathbb C$ it just means certain composites don't exist either.
We seek to model composites of paths of rewrites, and this is exactly the intended use of a virtual double category
Informally, a virtual double category (vdc) has the following data: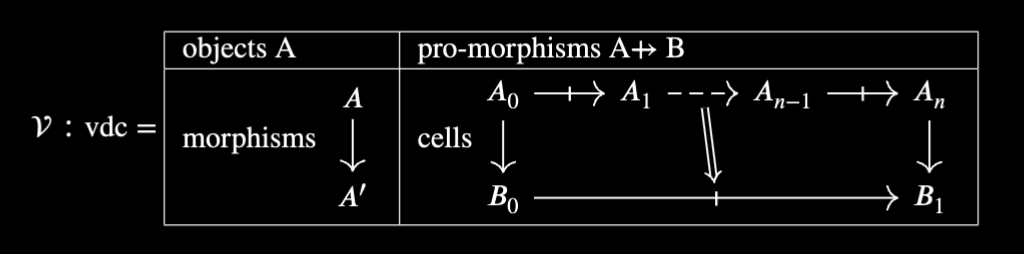 
${\mathcal V}$ has 1 categorical component ${\mathcal V}_{\text{mor}}$ containing the morphisms and 1 Graph component ${\mathcal V}_{\text{pro}}$ containing the pro-morphisms.
That is, we have two underlying functors $${\mathbb C\text{at}} \overset{(-)_{\text{mor}}}\longleftarrow{\text{vdc}}\overset{(-)_{\text{pro}}}\longrightarrow {\text{Graph}}$$Because pro-morphisms form a graph, they do not compose on the nose. Rather, the cells act as formal witnesses for the compositions of paths. In the case of DPO rewrites, these cells host the data of the pullbacks used to compose discussed above. "Virtual" double categories allow one to compose paths of "virtual" morphisms. Virtual morphisms are typically things that look like morphisms, but take extra data to compose, such as rewrites. We could track the pullback data using pseudocategories, however, the multiway system and virtual double categories emphasise paths of rewrites.
Informally a virtual double category of DPOs we should have:
$\to$ morphisms from $\mathbb C$
${\rlap{+}{\to}}$ pro-morphisms as DPO rewrites
$\square$ cells as pullbacks of paths of DPOs that are again DPOs
Note there is a difference between path concatenation, which exists in any graph, and path composition, which is defined by particular cells in a virtual double category. A cells in virtual double category really encodes the interaction between morphisms and paths of pro-morphisms. Composition is one of these cells in a vdc, they are the op-cartesian cells:
Op-cartesian cells satisfy a universal property in a vdc. Thus one need only specify the generic cells when defining a vdc, which is often easier.
All of the above details can be found in This Paper
We now begin the task of defining ${\text{DPO}}(\mathbb C)$ as a virtual double category
There is a related virtual double category to ${\text{DPO}}(\mathbb C)$ called ${\text{Span}}(\mathbb C)$, and an underlying functor ${\text{DPO}}(\mathbb C)\to {\text{Span}}(\mathbb C^\to)$ It forgets the universal properties of the DPO squares:
This underlying functor is likely induced by the underlying functor ${\mathbb C\text{at}}_{\text{bimark}} \to {\mathbb C\text{at}}$
$\mathbb C^\to$ helps to simplify things because the left diagram below is in $\mathbb C$, but the right diagram below is in $\mathbb C^\to$
composing the functors Span and $(-)^\to$ we have a functor $${\text{Span}}((-)^\to):{\mathbb C\text{at}} \to {\text{vdc}}$$ Likewise, we seek a functor $${\text{DPO}}:{\mathbb C\text{at}} \to {\text{vdc}}$$Formally, a virtual double category is an fc - multicategory, here is a great reference for multicategories
$fc$ refers to the "free category" monad on graphs (aka "path monad") $$(fc,i,\mu):{\text{Graph}} \to {\text{Graph}},\;\;fc(G) = \{\text{paths in }G\}$$
$G\overset{i} \to fc(G)$ is a trivial path, $fc(fc(G)) \overset\mu\to fc(G)$ is path concatenation.
An $fc$-multicatory forms the following diagram in the category ${\text{Graph}}$:
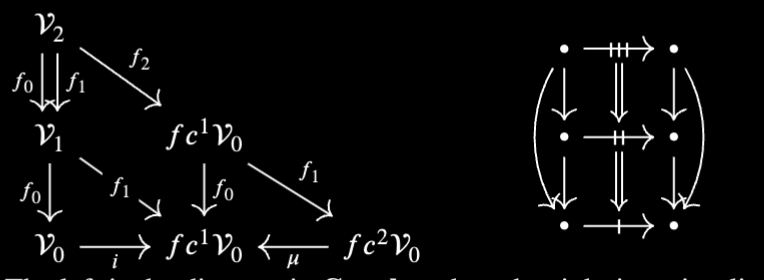
The left is the diagram in ${\text{Graph}}$ and on the right is a visualization of a composite of cells. Start on the above-left with an edge $\sigma\in{\mathcal V}_2$, following the diagram, as well as the diagram representing ${\text{Graph}}$ you will arrive at a composition of cells as shown in the above-right. note that the markings on the promorphisms is notation for paths of paths.
And so we come finally to the explicit definition of ${\text{DPO}}(\mathbb C)$
Def ${\text{DPO}}(\mathbb C)$
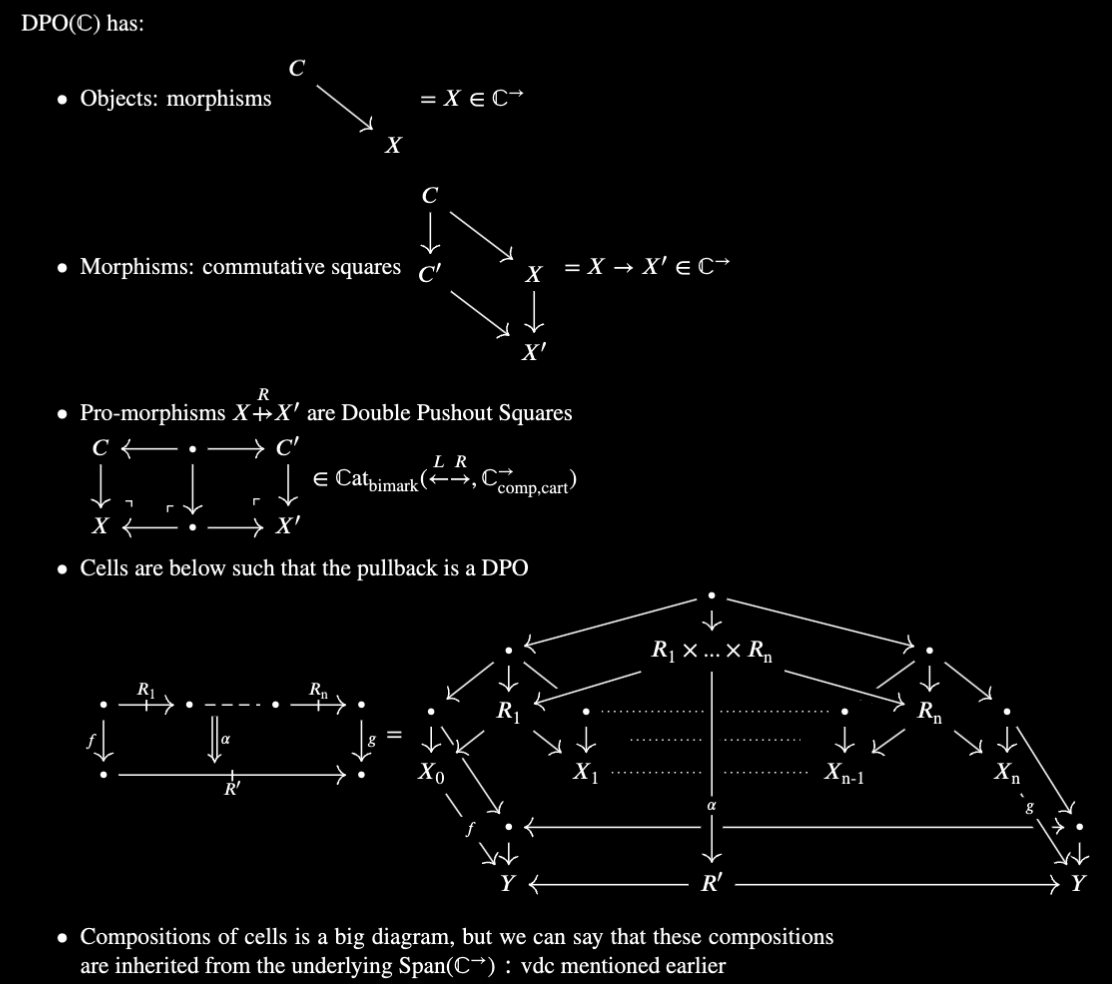
The point here is to hide the messy details a streamlined notation.
Again, These pullbacks need not exist, and when they do, they need not be DPOs. We consider only those paths of DPOs whose pullback is a DPO. If such a thing does not exist, then the cell on the left simply does not exist in ${\text{DPO}}(\mathbb C)$.
I will end with a remark about where this work is headed:
A case for representability
We now have an explicit definition for $\text{DPO}(\mathbb C)$. You might be skeptical because, well, we did not prove anything. This is because there is a way to define ${\text{DPO}}(\mathbb C)$ representably. That is, we seek the right structured category $\mathcal M$ to act as a meta-theory. And an object ${\text{DPO}}:\mathcal M$ that represents the concept of "double pushout" in the sense that the structured functors $\mathcal M({\text{DPO}},\mathbb C) \cong {\text{DPO}}(\mathbb C)$. I believe that something like marked virtual double categories may work, i.e. $\mathcal M = {\text{vdc}}_\ast$. Using exponential notation, we are asking for
$${\text{DPO}}(\mathbb C) \cong \mathbb C^{\text{DPO}}$$ Doing it this way, we can inherit most of the things we want to prove about $\mathbb C^{\text{DPO}}$ from the basic building blocks used to build ${\text{DPO}}$, and the properties of $\mathcal M$. Putting it this way makes something important, abundantly clear
${\text{DPO}} : \mathcal M$ is a choice of model for rewrites
Creating representative virtual double categories is a tricky task, you'll see it generalized in my thesis when it is published. Regardless, once we make this choice manifest -- as an object in a category -- it will be clear how one can upgrade both ${\text{DPO}}$ and $\mathcal M$.
An upgrade to ${\text{DPO}}$ might look like adding another layer to the rewriting choices:
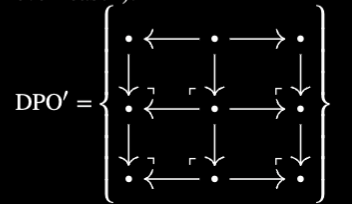
An upgrade to $\mathcal M$ might look like adding a notion of homotopical coherance. something like $\mathcal M$ = virtual double quasi categories
Attachments:
