Hi all,
I'm having a hard time computing the Delta of a European Put option using Mathematica. For those not in finance, i'm basically trying to computer a partial derivative of a function containing two other functions. I am setting the appropriate functions but once I try to compute it is not working.
Any help will be greatly appreciated!
I am trying to get this answer by calculating the partial derivative S from this function: 
From this function

Once again I need to calculate: 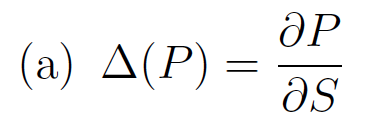 Here is my code
Here is my code
dplus[S_, [Sigma]_, q_, r_, t_, T_,
k_] := ((T - t) (r - q + [Sigma]^2/2) + Log[S/k])/(
Sqrt[T - t] [Sigma])
dminus[S_, [Sigma]_, q_, r_, t_, T_, k_] :=
dplus[S, [Sigma], q, r, t, T, k] - [Sigma] Sqrt[-t + T]
D[dplus[S, [Sigma], q, r, t, T, k ], S]
D[dminus[S, [Sigma], q, r, t, T, k ], S]
funtime[S_] := (
Se^(-q (T - t)) [CapitalPhi] (dplus[S, [Sigma], q, r, t, T,
k ])) - (Ke^(-r (T - t)) [CapitalPhi] (dminus[S, [Sigma], q,
r, t, T, k ]))
D[funtime[S], S]
But I am getting:
(Se^(-q (-t + T)) [CapitalPhi])/(S Sqrt[-t + T] [Sigma]) -
Ke^(-r (-t + T))
!(*SuperscriptBox[([CapitalPhi]dminus),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0", ",", "0", ",", "0", ",", "0", ",", "0", ",",
"0"}], ")"}],
Derivative],
MultilineFunction->None])[S, [Sigma], q, r, t, T, k]
Can anyone explain what is going on? I can successfully get partial derivatives from the first 2 parameters (Dplus and Dminus), but once I try to get the partial derivative from my function, "funtime", it's not coming together. Any help will be greatly appreciated! I have attached my mathematica file for anyone trying to help.
Thanks!
 Attachments:
Attachments: