Just to attract attention. This is a real problem in physics and it involves pseudoscalar meson photoproduction in hadron spectroscopy. We use CGLN amplitudes to describe the problem. 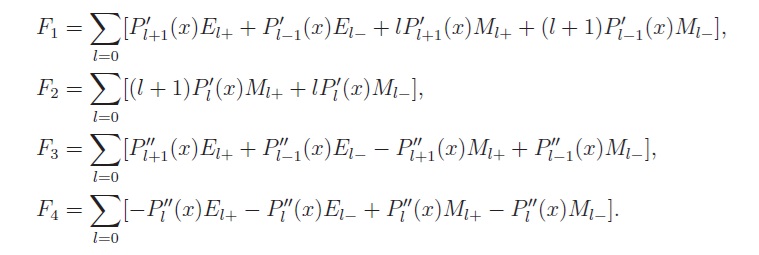These amplitudes create 16 observables as bilinears of these amplitudes. 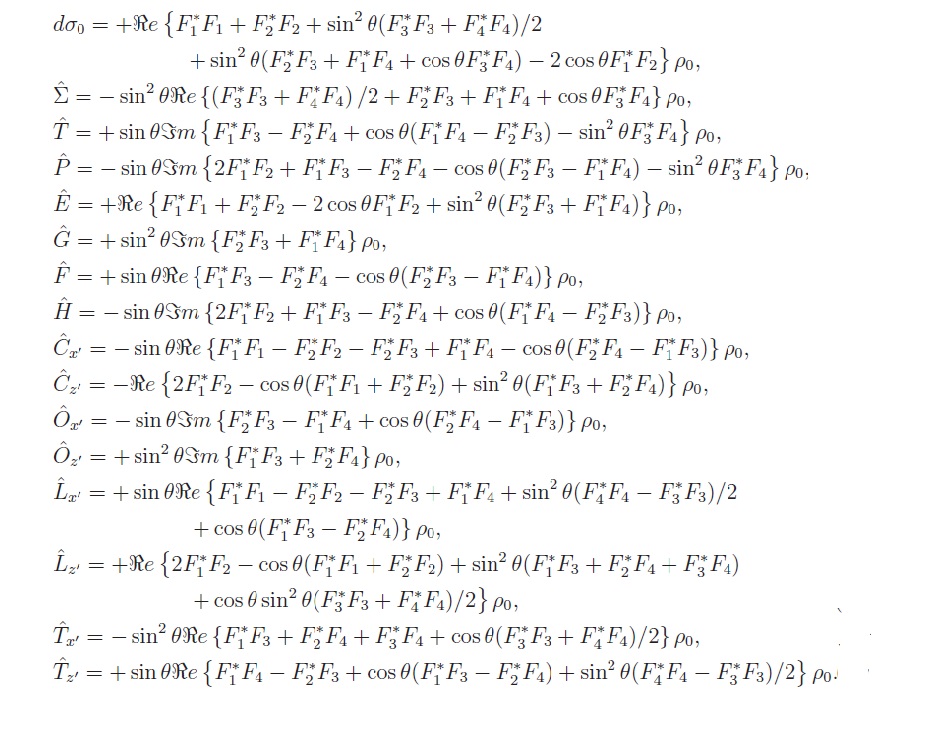We study the case where Lmax=1.
The task: obtain unknown complex multipoles (E0+, M1-, E1+, M1+) from observables.

Method:

1. We generate numeric values of observables from chosen complex multipoles (8 real numbers)
2. We fit these numbers with 8 real parameters
3. We expect to restore original multipoles

Problem: Because of physical reasons, observables are given as billinears of amplitudes, so the overall phase cannot be determined.

This problem is solved by introducing three constraining equations.

I first fit one observable d$\sigma_0$.

The main problem to be solved is that the minimizing function (square of the difference between numeric data and theoretical value) should be exactly zero to obtain the result, and this function has a lot of local minima and is very sensitive to the precision of the machine.

I use FindMinimium as the problem is constrained fit.

Enclosed is the code with descriptions.

The main issue is that I know, and can calculate the Chi2 within the standard precision of the machine, but my minimization never finds this value.

The code is enclosed.

This is a research in progress, and results can be published. If someone contributes, he is welcome to be the co-author.