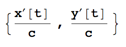If coordinate vector of a point is given by
coor[t_] := {Quantity[x[t], "Meters"], Quantity[y[t], "Meters"]}
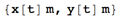
and time is defined as
time = Quantity[t, "Seconds"]
and constant speed as
speed = Quantity[c, "Meters"/"Seconds"]
then time derivative of coordinate vector will give velocity in proper units:
D[coor[t], time]
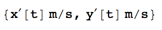
which also can be rescaled as dimensionless
D[coor[t], time]/speed