A function is to be constructed that, given an input of a positive integer value m, automatically enumerates all possible cases. Starting with an arithmetic sequence of length 4*m + 2, two terms are removed leaving 4m terms, which are then evenly divided into m groups, each consisting of 4 numbers. It is required that the 4 numbers in each group form their own arithmetic sequence. The function should generate all combinations of the two removed terms and the corresponding m groups of four numbers forming arithmetic sequences.

To clarify the problem statement further, let's break down the requirements:

1. An arithmetic sequence of length 4*m + 2 is created.
2. Two terms from this sequence are removed.
3. The remaining 4m terms are divided into m groups, each containing exactly 4 terms.
4. Each of these groups must also be an arithmetic sequence.
5. The function should output all possible combinations of the two removed terms and the resulting groups of four numbers that form arithmetic sequences.

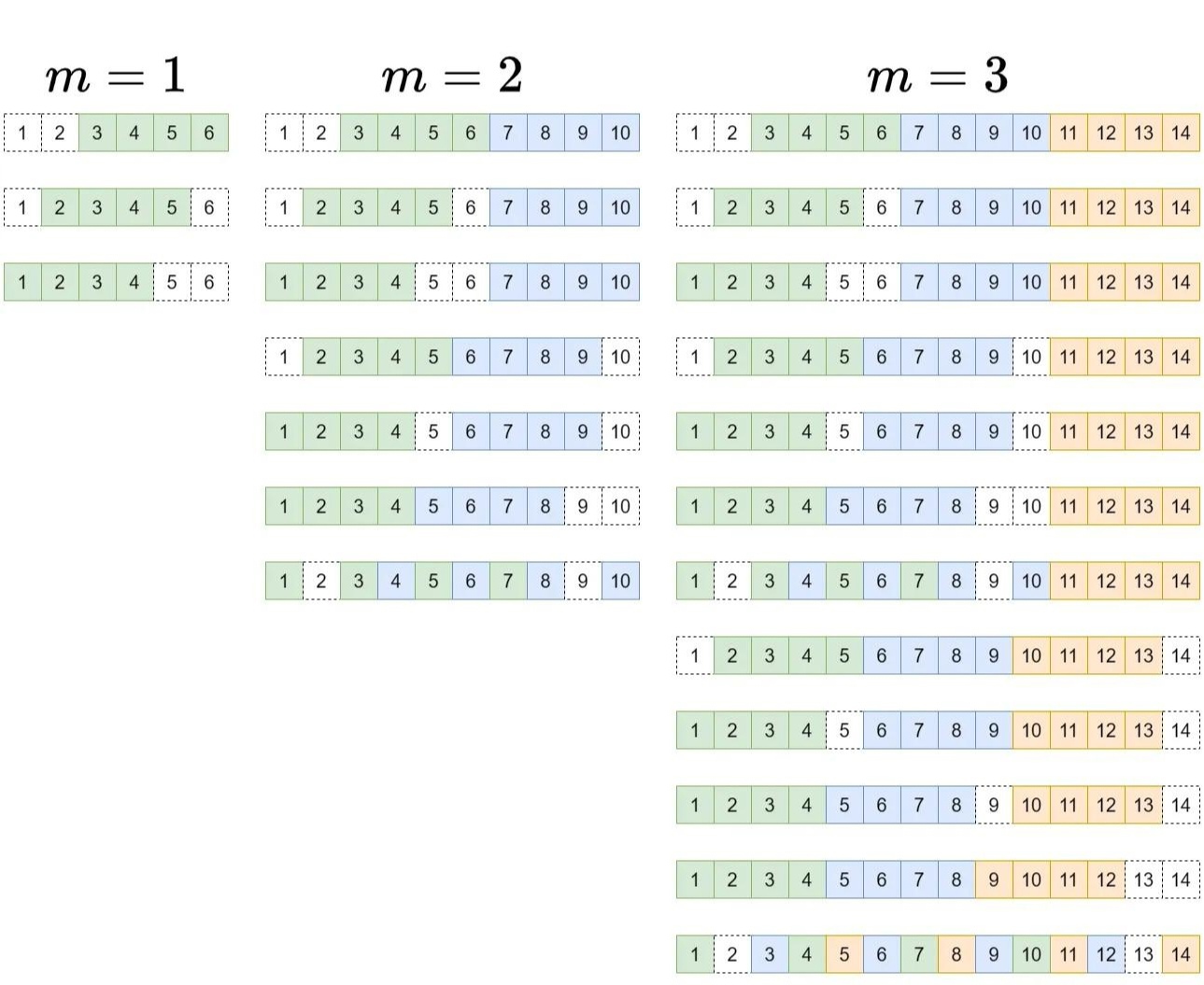
Finally, represent each outcome using the grid diagram shown above.

f[m_] := Module[{S, graph}, S = Range[4 m + 2];
  graph = 
   RelationGraph[DisjointQ, 
    Select[Subsets[S, {4}], Equal @@ Differences@# &]];
  GroupBy[FindClique[graph, Length /@ FindClique[graph], All], 
   Complement[S, Join @@ #] &]]

grid[m_] := 
 Grid[MapIndexed[{#2[[1]], Multicolumn[#, 2, Spacings -> 1]} &, 
   Map[Function[x, 
     TextGrid[
      Range[4 m + 2] /. 
       a -> Alternatives @@ 
         Thread[a : Complement[Range[4 m + 2], Join @@ x] :> 
           Highlighted[a, FrameMargins -> 0]], Frame -> All, 
      FrameStyle -> Gray, 
      Background -> {None, None, 
        Join @@ MapIndexed[
          Thread[Thread[{1, #}] -> 
             Lighter[Hue[(Tr@#2 - 1)/Length@x], 0.85]] &, x]}]], 
    Values@f[m], {2}]], Alignment -> Left, Spacings -> {Automatic, 1}]

The above code is not producing results correctly. How can it be corrected or modified to achieve the correct output?