Introduction

During my time at Lawrence Technological University, researching under Dr. Bhubanjyoti Bhattacharya, I developed code using Wolfram Mathematica to help visualize the 2-dimensional rotation matrix. The 2D rotation matrix rotates an object by an angle and determines its new components:

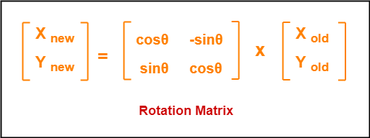
My code uses algebraic and trigonometric calculations to animate both a pair of axes rotating about a vector and the vector's components.

Program Breakdown

a = Graphics[Arrow[{{0, 0}, {5, 5}}], Axes -> True]; 
axis2vectorangle = ArcTan[1];

The variable, "a," represents a set vector in 2-dimensional space. The variable, "axis2vectorangle," represents the angle between the original axis and set vector; because the vector's x and y coordinates are equal to each other, "axis2vectorangle" equals the inverse tangent of '1.'

x[[Theta]_] := 
  Graphics[{Dashed, 
    Line[{{5, 
       5}, {-5 Sqrt[2]
         Sin[axis2vectorangle - [Theta] Degree] Sin[[Theta] Degree],
        5 Sqrt[2]
         Sin[axis2vectorangle - [Theta] Degree] Cos[[Theta]
Degree]}}]}];

y[[Theta]_] := 
  Graphics[{Dashed, 
    Line[{{5, 
       5}, {5 Sqrt[2]
         Cos[axis2vectorangle - [Theta] Degree] Cos[[Theta] Degree],
        5 Sqrt[2]
         Cos[axis2vectorangle - [Theta] Degree] Sin[[Theta] 
Degree]}}]}];

p[[Theta]_] := 
  Show[{a, x[[Theta]], y[[Theta]], 
    Plot[{Tan[[Theta] Degree] x, 
      Tan[([Theta] + 90) Degree] x}, {x, -10, 10}, 
     PlotRange -> {-10, 10}, Axes -> True, AxesStyle -> Dashed, 
     AspectRatio -> 1, PlotStyle -> {Gray}]}];

figure = 
  Animate[p[[Theta]], {{[Theta], 45}, 0, 360}, 
   ControlPlacement -> Top];

The functions x[[Theta]] and y[[Theta]] define the x and y components, respectively, of the vector, with respect to an axis rotated by [Theta] degrees.

x[[Theta]]

Multiplying the length of "a," '5Sqrt[2],' by the sine of [axis2vectorangle - [Theta] degrees] results in the hypotenuse of the x and y components of the vector's x component, post-axis-rotation. Then, multiplying by the sine of [Theta] degrees yields the x coordinate, while multiplying by the cosine of [Theta] degrees yields the y coordinate.

y[[Theta]]

Using the same length of the vector, "a," but multiplying by the cosine of [axis2vectorangle - [Theta] degrees] results in the hypotenuse of the x and y components of the vector's y component, post-axis-rotation. Then, multiplying by the cosine of [Theta] degrees yields the x coordinate, while multiplying by the sine of [Theta] degrees yields the y coordinate.

Finally, p[[Theta]] graphs "a," x[[Theta]], y[[Theta]], and the pair of axes rotated by an angle [Theta]. This function is animated to clearly visualize the 2D rotation group through the rotation of a pair of axes.

Animation

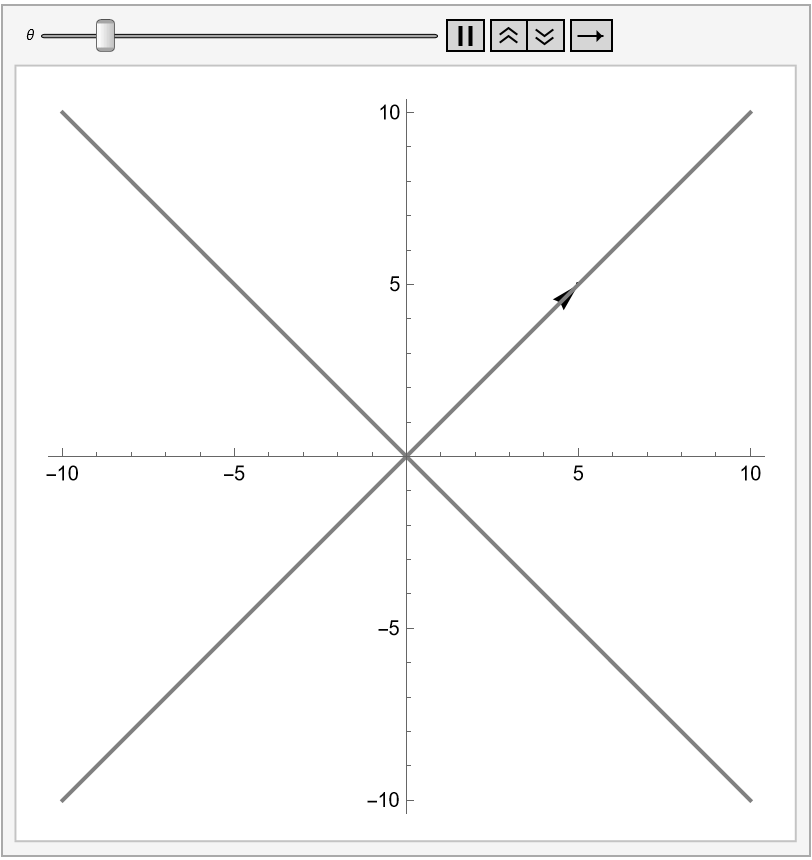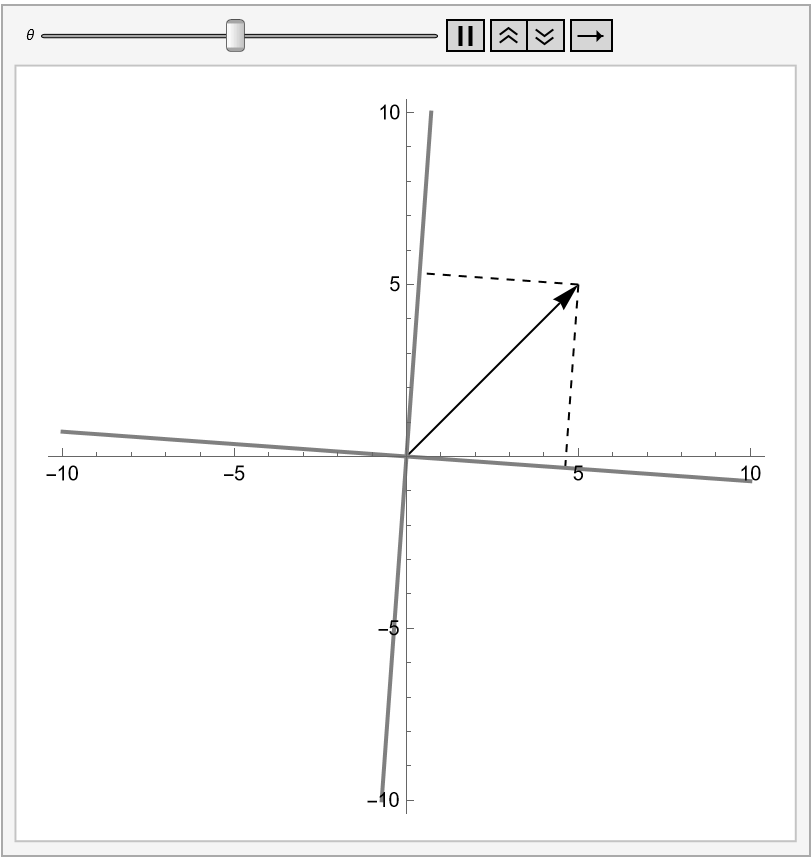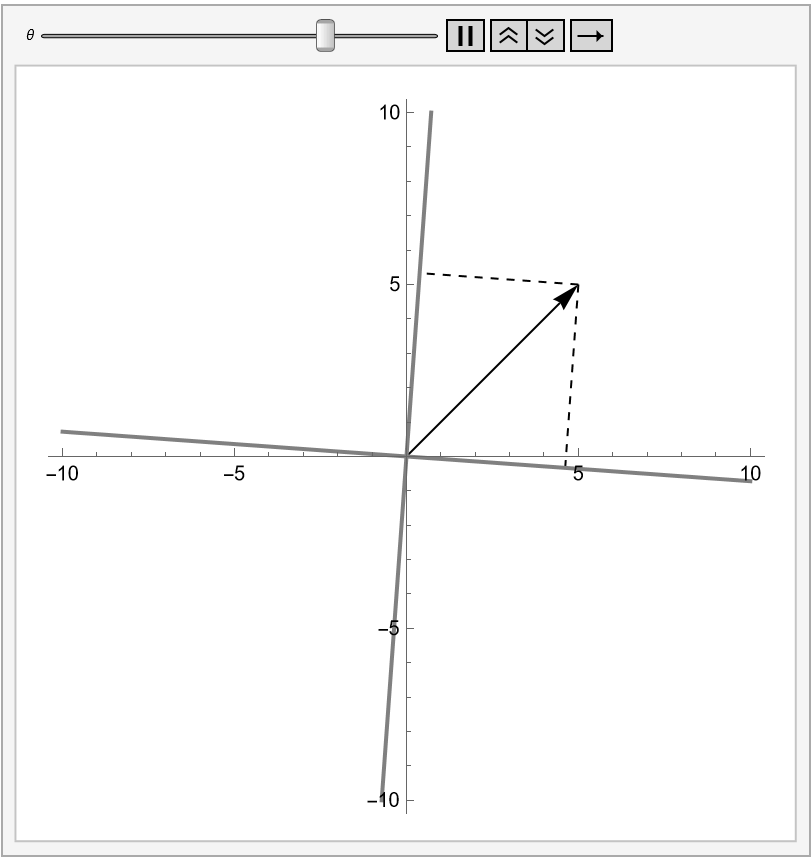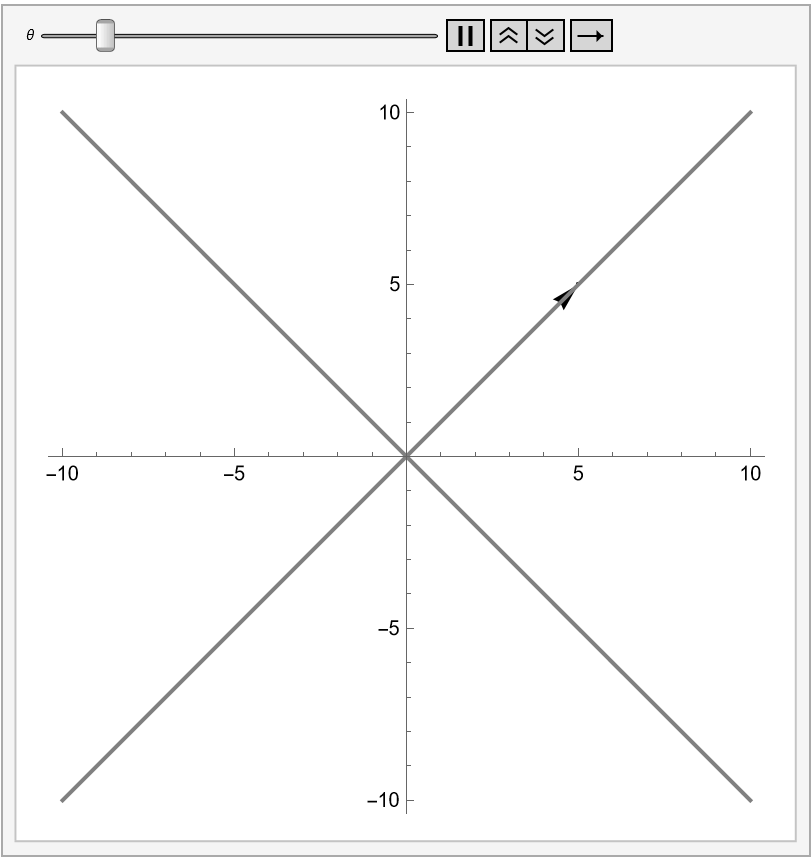
Conclusion

Generally, this code uses algebraic and trigonometric calculations in an attempt to help visualize the 2D rotation matrix for those unfamiliar with the concept. Attached is a notebook that contains this program and the same breakdown text interspersed through it.

Attachments:

2d rotation group.nb