Often of interest are stochastic processes with absorbing boundaries (states). However, Mathematica does not natively include functionality to deal with absorption.

In one spatial dimension there is a nice solution: prior solution

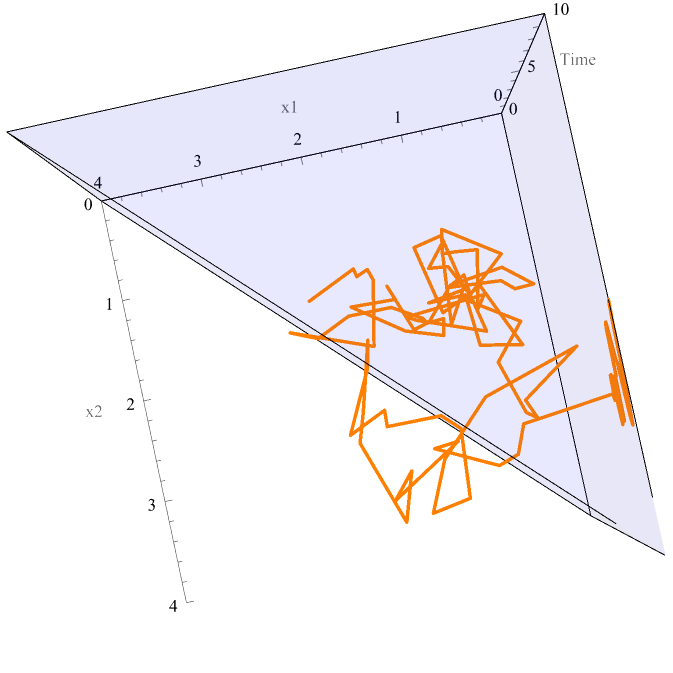
Yet, I'm considering a situation where the process evolves with absorbing boundaries in multiple dimensions. In particular, I'm considering a regular simplex. If the process hits a boundary it cannot leave but continues to evolve until it hits a vertex.

The method I'm using is indicator functions that stop the dynamics in certain dimensions when a boundary is crossed. It works well for boundaries aligned with Cartesian coordinates, but is verbose otherwise; particularly, considering I want to scale this to higher dimension simplices. The pictures below illustrate.

ClearAll["Global`*"]

\[Theta] = .50;
\[Mu] = {1, 2};

\[Eta] = 4.;
dim = 2;


Tmax = 10.;
dt = .1;

xs = Table[Subscript[x, i], {i, dim}];
xts = Map[(#[t] &), xs];
wprocs = 
  Table[Subscript[w, i] \[Distributed] WienerProcess[], {i, dim}];


\[CapitalOmega] = 
  ImplicitRegion[
   Evaluate[Total[xs] <= \[Eta] \[And] Apply[And, Thread[xs >= 0]]], 
   Evaluate[xs]];


eqs = Table[\[DifferentialD](Subscript[x, i][
       t]) == (\[Theta] (\[Mu][[i]] - 
          Subscript[x, i][
           t]) \[DifferentialD](t) + \[DifferentialD](Subscript[w, i][
          t]))*UnitStep[
      Subscript[x, i][t] (\[Eta] - Subscript[x, i][t])], {i, dim}];


proc = ItoProcess[eqs, xts, {xs, RandomPoint[\[CapitalOmega]]}, t, 
   wprocs];
paths = Clip[RandomFunction[proc, {0, Tmax, dt}], {0, \[Eta]}];


trad = ({#2[[1]], #2[[2]], #1} &) @@@ Flatten[paths["Paths"], 1];

regionPlot = 
  RegionPlot3D[
   Total[{x1, x2}] <= \[Eta] && x1 >= 0 && x2 >= 0, {x1, 
    0, \[Eta]}, {x2, 0, \[Eta]}, {t, 0, Tmax}, 
   PlotStyle -> Directive[Opacity[0.05], Blue],
   Mesh -> None, Boxed -> False, AxesLabel -> {"x1", "x2", "Time"}, 
   PlotRange -> {{0, \[Eta]}, {0, \[Eta]}, {0, Tmax}}, 
   PlotTheme -> "Scientific"];
trajectoryPlot = 
  ListLinePlot3D[trad, PlotTheme -> "Scientific", 
   BoxRatios -> {1, 1, GoldenRatio}, PlotStyle -> {Orange, Thick}];

Show[regionPlot, trajectoryPlot]

Desired behaviour:

Undesired behaviour: