I think also the safest way is to format it at the end for displaying. Here is a quick function hacked to do this. If you find any bugs, please let me know. This is just for final display.
formatIt[Expand[(z + 1/z)^5], z]
formatIt[Normal@Series[Sin[x], {x, 0, 10}], x]
formatIt[Expand[(z + 1/z)^4], z]
formatIt[1, z]
formatIt[-1 + z^3, z]
formatIt[Expand[(z + 1/z)^6, z], z]
Which gives
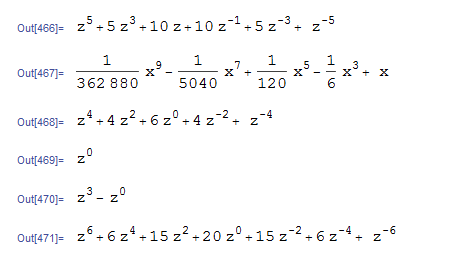
ps. I am not too good in parsing and patterns with Mathematica, and I am sure this can be done much better, but just a proof of concept.
formatIt[r_, z_] := Module[{x, e, c, n, o},
(*nma, version 8/23/14, 2 PM*)
fixMiddle[c_] := If[Sign[c] < 0, If[Abs[c] == 1, Row[{"-", Spacer[1]}], c], Row[{"+", Spacer[1], If[c != 1, c]}]];
fixFirst[c_] := If[Sign[c] < 0, If[Abs[c] == 1, Row[{"-", Spacer[1]}], c], If[c == 1, Sequence @@ {}, c]];
o = If[Head[r] === Plus, r, List@r]; (*to handle single terms*)
o = Cases[lis, Alternatives[x_. Power[z, e_.], Times[x_, Power[z, e_.]], Dot[x_, e_: 0]] :> {x, e}];
o = Sort[o, #1[[2]] > #2[[2]] &];
o = {#[[1]], If[#[[2]] < 0, Superscript[z, #[[2]]], If[#[[2]] > 0, z^#[[2]], z^"0"]]} & /@ o;
o = MapIndexed[{n = First[#2]; c = #1[[1]]; e = #1[[2]];
Row[{If[n == 1, fixFirst[c], fixMiddle[c]], Spacer[2], e, Spacer[1]}]} &, o];
Row[Flatten[o]]
];