I think also the safest way is to format it at the end for displaying. Here is a quick function hacked to do this. If you find any bugs, please let me know. This is just for final display.

   formatIt[Expand[(z + 1/z)^5], z]
   formatIt[Normal@Series[Sin[x], {x, 0, 10}], x]
   formatIt[Expand[(z + 1/z)^4], z]
   formatIt[1, z]
   formatIt[-1 + z^3, z]
   formatIt[Expand[(z + 1/z)^6, z], z]

Which gives

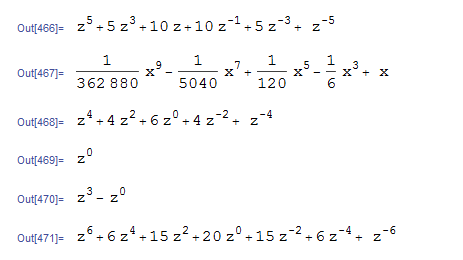
ps. I am not too good in parsing and patterns with Mathematica, and I am sure this can be done much better, but just a proof of concept.

  formatIt[r_, z_] := Module[{x, e, c, n, o},
     (*nma, version 8/23/14, 2 PM*)
     fixMiddle[c_] := If[Sign[c] < 0, If[Abs[c] == 1, Row[{"-", Spacer[1]}], c], Row[{"+", Spacer[1], If[c != 1, c]}]];
     fixFirst[c_] := If[Sign[c] < 0, If[Abs[c] == 1, Row[{"-", Spacer[1]}], c], If[c == 1, Sequence @@ {}, c]];
     o = If[Head[r] === Plus, r, List@r]; (*to handle single terms*)
     o = Cases[lis, Alternatives[x_. Power[z, e_.], Times[x_, Power[z, e_.]], Dot[x_, e_: 0]] :> {x, e}];
     o = Sort[o, #1[[2]] > #2[[2]] &];
     o = {#[[1]], If[#[[2]] < 0, Superscript[z, #[[2]]], If[#[[2]] > 0, z^#[[2]], z^"0"]]} & /@ o;
     o = MapIndexed[{n = First[#2]; c = #1[[1]]; e = #1[[2]]; 
         Row[{If[n == 1, fixFirst[c], fixMiddle[c]], Spacer[2], e, Spacer[1]}]} &, o];
     Row[Flatten[o]]
     ];

Fixed. Forgot about the z^0 case. Again, this is just proof of concept. The parsing can be done better and in a much more robust way. Any other bugs, please let me know.

As I explained in my previous comments, assuming a behaviour is not good enough for me. But even with this assumption, in

Expand[(y + z)^4] 

and

Expand[(y + z)^4] /. y -> 1/z

the order is changing with the replacement. The binomial expansion order is not kept. Mathematica recognizes that the result is of a special form, and does undocumented (or at least I did not find the relevant documentation) reordering for the output after the replacement. Again, this is not a problem for computational use of Mathematica, rather it is a strength that it recognizes so many forms of expressions, but it would be nice to know a way of forcing it not to do the reordering in this case after the replacement.

Yes, of course I can write my own algorithms, which is what I ended up doing in this case and also in several other cases (e.g. I am drawing circular arcs using ParametricPlot). I now use

CoefficientList[(z + 1/z)^4*z^4, z]

because it is well documented, and I can get all the information I need from the output.