I think also the safest way is to format it at the end for displaying. Here is a quick function hacked to do this. If you find any bugs, please let me know. This is just for final display.

   formatIt[Expand[(z + 1/z)^5], z]
   formatIt[Normal@Series[Sin[x], {x, 0, 10}], x]
   formatIt[Expand[(z + 1/z)^4], z]
   formatIt[1, z]
   formatIt[-1 + z^3, z]
   formatIt[Expand[(z + 1/z)^6, z], z]

Which gives

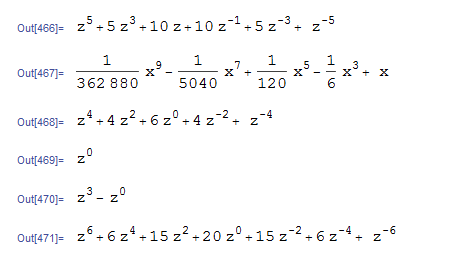
ps. I am not too good in parsing and patterns with Mathematica, and I am sure this can be done much better, but just a proof of concept.

  formatIt[r_, z_] := Module[{x, e, c, n, o},
     (*nma, version 8/23/14, 2 PM*)
     fixMiddle[c_] := If[Sign[c] < 0, If[Abs[c] == 1, Row[{"-", Spacer[1]}], c], Row[{"+", Spacer[1], If[c != 1, c]}]];
     fixFirst[c_] := If[Sign[c] < 0, If[Abs[c] == 1, Row[{"-", Spacer[1]}], c], If[c == 1, Sequence @@ {}, c]];
     o = If[Head[r] === Plus, r, List@r]; (*to handle single terms*)
     o = Cases[lis, Alternatives[x_. Power[z, e_.], Times[x_, Power[z, e_.]], Dot[x_, e_: 0]] :> {x, e}];
     o = Sort[o, #1[[2]] > #2[[2]] &];
     o = {#[[1]], If[#[[2]] < 0, Superscript[z, #[[2]]], If[#[[2]] > 0, z^#[[2]], z^"0"]]} & /@ o;
     o = MapIndexed[{n = First[#2]; c = #1[[1]]; e = #1[[2]]; 
         Row[{If[n == 1, fixFirst[c], fixMiddle[c]], Spacer[2], e, Spacer[1]}]} &, o];
     Row[Flatten[o]]
     ];

Fixed. Forgot about the z^0 case. Again, this is just proof of concept. The parsing can be done better and in a much more robust way. Any other bugs, please let me know.

As I explained in my previous comments, assuming a behaviour is not good enough for me. But even with this assumption, in

Expand[(y + z)^4] 

and

Expand[(y + z)^4] /. y -> 1/z

the order is changing with the replacement. The binomial expansion order is not kept. Mathematica recognizes that the result is of a special form, and does undocumented (or at least I did not find the relevant documentation) reordering for the output after the replacement. Again, this is not a problem for computational use of Mathematica, rather it is a strength that it recognizes so many forms of expressions, but it would be nice to know a way of forcing it not to do the reordering in this case after the replacement.

Yes, of course I can write my own algorithms, which is what I ended up doing in this case and also in several other cases (e.g. I am drawing circular arcs using ParametricPlot). I now use

CoefficientList[(z + 1/z)^4*z^4, z]

because it is well documented, and I can get all the information I need from the output.

I am trying to write CDF notes with demonstrations. If something is "unlikely to change" or (as in the documentation of Sort[]) "usually ..." is not good enough. This is not a problem with usual use of Mathematica, because one can react if something is not as we would expect. But CDF is a different thing. I am producing something which I have to be sure behaves as I intend it to behave 2-3 years from now. I can play with formatting, but the question remains, will future versions format it the same way? In this case, this is a Laurent polynomial in one variable with numbers as coefficients, but the order is not according to the degrees in that variable. The constant term is first, but it should be in the middle. I think, it is because what is written in the Sort[] documentation, that least complex terms are first, but still there is this "usually" in the documentation, which I don't understand. In any case, since my post I could sort out what I want with the use of CoefficientList[], where the documentation is quite explicit about the order.

Polynomials are always output in the increasing order of powers. If you wish to see the highest power to the left (as we might do when handwriting), one might try the following.

ClearAttributes[Plus, Orderless](*Remove the "Orderless" attribute of Plus*);
(*Apply the orderless*)Plus @@(List @@ (*Change head from Plus to List*)Expand[(z + 1/z)^5])

By removing the builtin "Orderless", we tell the Plus sign that it must keep the user provided order.

I don't want the order changed for display purposes. I want to be sure, that what I get as an output now, it will be the same in future versions of Mathematica. Apparently Mathematica uses some algorithms to order expressions, but these are hidden from the user.

Thanks, but this link did not answer my question. The "OrderedForm" operation there did not put the terms of (z+1/z)^4 in increasing powers of z. However, my main question is: Can I rely on the behaviour I see now to stay like this in future versions of Mathematica? In the documentation I do not see any reference as to how Expand[] orders the output, and in this case it is not the normal order of the binomial expansion. I am writing demonstrations to use by others, so I cannot rely on experimenting with the output. I need a guarantee that it will always be the same. Mathematica is very powerful, but because of this, calculations happen behind the scene, and although the output is nice, I don't see how I can control it.