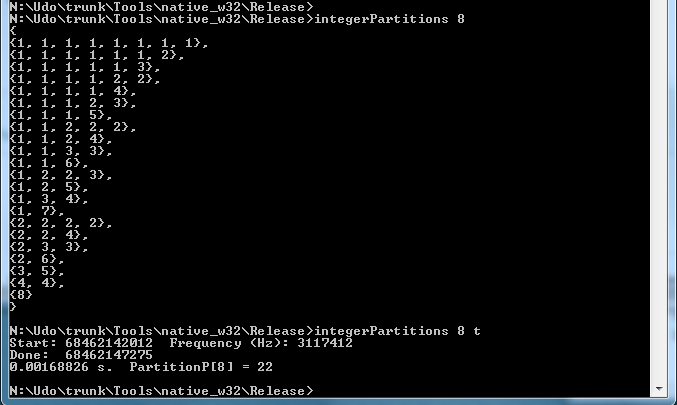
Following J Kelleher Ascending Partitions here is a code snippet implementing it with Mathematica

(* show (ii) *)
Clear[ruleAsc]
ruleAsc[n_Integer?Positive] := 
 Block[{a = Table[0, {Max[2, n]}], k = 1, x, y, q, r = {{}}},
  a[[2]] = n;
  While[k > 0,
   {x, y} = a[[k ;; k + 1]] + {1, -1};
   If[q = [LeftFloor]y/x[RightFloor]; q > 0,
    a[[k ;; k + q - 1]] = x;
    k += q;
    a[[k]] = x (1 - q) + y, (* else *)
    a[[k]] = x + y
    ];
   r = Join[r, {a[[1 ;; k]]}];
   --k;
   ];
  Rest[r]
  ]

it runs not too fast

In[3]:= First[Timing[ruleAsc[40]]]
Out[3]= 20.436131

so the question was, can Compile made it run faster? As it stands, it does not compile because of the TensorForm error message: get rid of the sublists and use 0 as separator between partitions.

In[6]:= Needs["CCompilerDriver`"]

In[7]:= $CCompilerDefaultDirectory
Out[7]= "C:UsersJoeyAppDataRoamingMathematicaSystemFilesLibraryResourcesWindows-x86-64"

In[8]:= Remove[raC]
    raC = Compile[{{n, _Integer}}, 
      Module[{a = Table[0, {Max[2, n]}], k = 1, x, y, q, r = {0}},
       a[[2]] = n;
       While[k > 0,
        {x, y} = a[[k ;; k + 1]] + {1, -1};
        If[q = [LeftFloor]y/x[RightFloor]; q > 0,
         a[[k ;; k + q - 1]] = x;
         k += q;
         a[[k]] = x (1 - q) + y, (* else *)
         a[[k]] = x + y
         ];
        r = Join[r, a[[1 ;; k]], {0}];
        --k
        ];
       Most[Rest[r]]
       ], CompilationTarget -> "C"]

One uses CompilationTarget -> "C" to take advantage of the Visual Studio 2008 C/C++ compiler installed here und the runtime is ...

In[10]:= First[Timing[raC[40]]]
Out[10]= 78.515303

In[11]:= First[Timing[IntegerPartitions[40]]]
Out[11]=  0.015600

In[12]:= %10/%11
Out[12]=  5033.

In[15]:= %10/%3
Out[15]= 3.841985

nearly four times slower as the ruleAsc script and around five thousand times slower as the built in functions.

What is Compile doing here, given that it's possible to implement ruleAsc with the same compiler to run faster than the built-in function IntegerPartitions as seen below:

In[5]:= Table[{o, PartitionsP[o], First[Timing[IntegerPartitions[o]]]}, {o, 1, 71, 10}]
Out[5]= {{1,         1,  0.},   (* C/C++:  1, 0.00203534 s *)
          {11,      56,  0.},   (* C/C++: 56, 0.00199332 s *)     
          {21,     792,  0.},   (* C/C++: 792, 0.00188426 s *)
          {31,    6842,  0.},   (* C/C++: 6842, 0.0039876 s *)
          {41,   44583,  0.015600},   (* C/C++: 44583, 0.0123452 s *)
          {51,  239943,  0.046800},   (* C/C++: 239943, 0.0524573 s *)
          {61, 1121505,  0.296402},   (* C/C++: 1121505, 0.245616 s *)
          {71, 4697205,  1.466409}}   (* C/C++: 4697205, 0.977096 s *)

the C/C++ runtimes have been copied from the following into the comments for convenience.

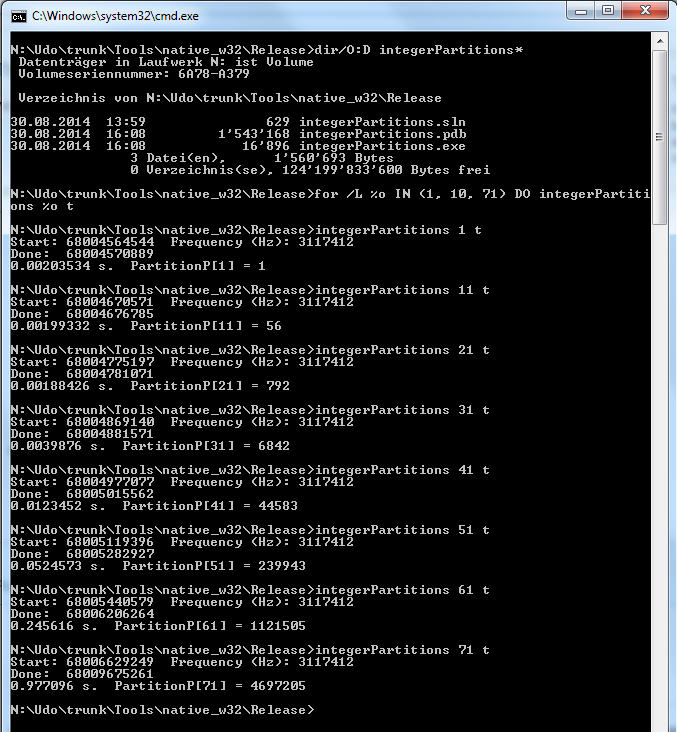
51 is a bit slower; the runtimes vary from run to run; in this code the parameter t suppresses the display of the result only: