Hello Wolfram Community!

I’m working on implementing a custom loss function in Mathematica to apply a weighted least squares approach to neural networks. Specifically, I’d like to modify the standard mean squared error (MSE) loss function to incorporate weights, so it can account for the varying importance of different data points in training.

Objective The standard MSE loss function simply calculates the average squared difference between the actual values and the predicted values. I’d like to generalize this to a weighted mean squared error, or weighted least squares (WLS), by including a weight for each data point. This way, the loss function can emphasize certain points over others, depending on their assigned weights.

What I’ve Tried I’ve set up a basic neural network in Mathematica using NetTrain, but I'm unsure how to properly integrate the weighted loss function. My data have a clear outlier to test the effect of small and big weights.

Code So Far

We first run do a regression with smooth with a clear outlier

data = {0. -> {0., 1.}, 0.2 -> {0.2, 1.3313}, 0.4 -> {0.4, 1.12215}, 
   0.6 -> {0.6, 1.74427}, 0.8 -> {0.8, 2.10747}, 1. -> {1., 2.08546}, 
   1.2 -> {1.2, 2.11952}, 1.4 -> {1.4, 2.43156}, 
   1.6 -> {1.6, 2.90507}, 1.8 -> {1.8, 2.92229}, 2. -> {2., 3.69933}, 
   2.2 -> {2.2, 2.88064}, 2.4 -> {2.4, 4.13182}, 
   2.6 -> {2.6, 3.48614}, 2.8 -> {2.8, 5.00537}, 3. -> {3., 4.08107}, 
   3.1 -> {3.1, 9.2469}, 3.2 -> {3.2, 4.61768}, 3.4 -> {3.4, 4.7964}, 
   3.6 -> {3.6, 5.26735}, 3.8 -> {3.8, 5.54625}, 4. -> {4., 5.71246}, 
   4.2 -> {4.2, 6.17115}, 4.4 -> {4.4, 6.97052}, 
   4.6 -> {4.6, 7.64505}, 4.8 -> {4.8, 7.2061}, 5. -> {5., 8.18249}};

deep = NetChain[{100, LinearLayer[100], Tanh, 2}]; wGraph = 
 NetGraph[<|"net" -> deep, "loss" -> MeanSquaredLossLayer[], 
   "times" -> ThreadingLayer[Times]|>, {"net" -> 
    "loss", {NetPort["Weight"], "loss"} -> 
    "times" -> NetPort["WeightedLoss"]}];
dataset := <|"Input" -> data[[All, 1]], "Target" -> data[[All, 2]], 
   "Weight" -> weight|>;

finalplot := 
 With[{result = 
    NetTrain[wGraph, dataset, LossFunction -> "WeightedLoss", 
     MaxTrainingRounds -> 5000, BatchSize -> 200]}, 
  final = NetExtract[result, "net"]; 
  Show[ListPlot[{Flatten[Table[final@{x}, {x, 0., 5., 0.2}], 1], 
     data[[All, 2]][[All, 1 ;; 2]]}, PlotStyle -> {Blue, Orange}]]]

weight = Table[0.1, Length[data]]; finalplot

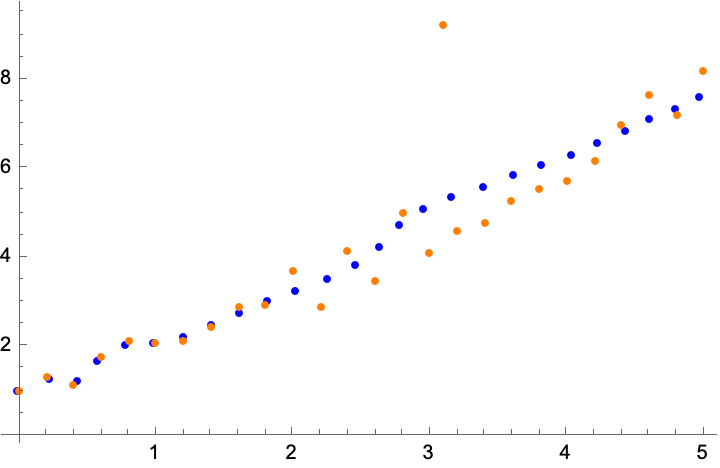
Let us look at the effect of having a very small weight

weight = 
ReplacePart[Table[0.1, Length[data]], 17 -> 0.000001]; finalplot here

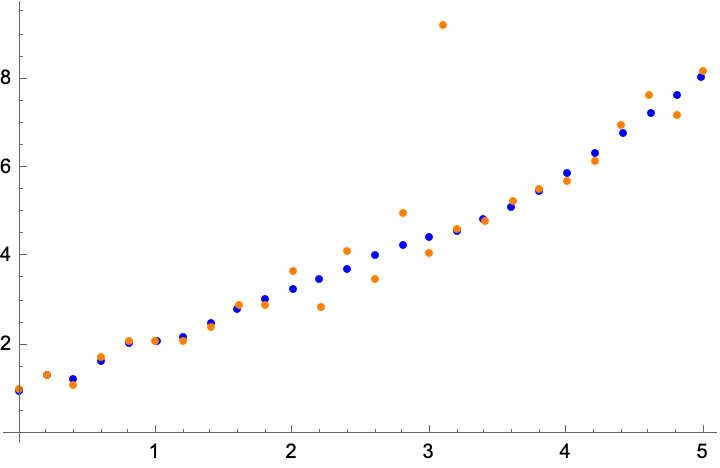
And now a big weight

weight = 
ReplacePart[Table[0.1, Length[data]], 17 -> 40.]; finalplot

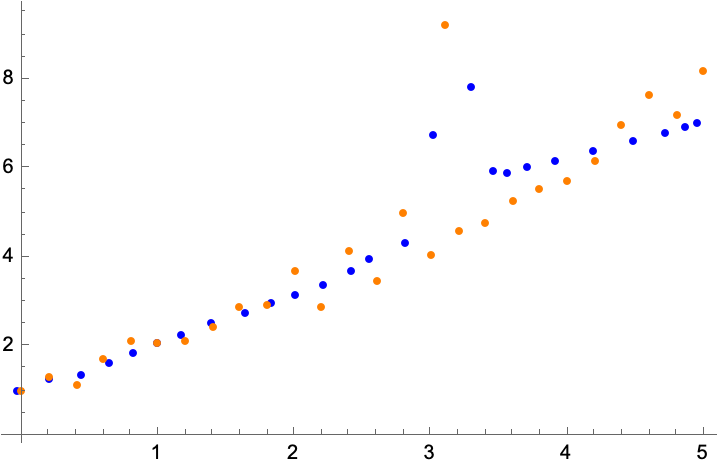
There is a clear effect both when the weight is small and big.

Question Could anyone suggest how to integrate weights in a way that NetTrain can handle during each training step? I would also appreciate any tips on improving this code or best practices for implementing custom loss functions in Mathematica.

Thank you in advance for your help!