Results from further research unveiling the utility of the MRB constant

A notable instance was when

Dr. Michele Nardelli,

established the connection of the MRB constant to the study of Geophysics.

One of his remarkable discoveries is shown in this link and worked in this notebook.

According to Prof Nardelli, the equation above is 98.9 percent near to the mass of candidate glueball f ₀ (1710) scalar meson.

The significance of this estimation (by Gemini AI)

A z-score of approximately 1.734 indicates that the new value x ≈ 1.0005787037 is about 1.734 standard deviations above the mean of the data set ranging from 0.00000001 to 0.999999999.

For the estimate of the mass of candidate glueball f ₀ (1710) scalar meson, the fraction 1729/1728 ≈ 1.0005787037 is about 1.734 standard deviations above the mean of the set of real numbers from 0.00000001 to 0.999999999. This indicates that the new value is somewhat significant and lies within the range where many data points fall in a normal distribution.

Similar to how I took claim to the Value that is named after me, Nardelli has a constant: The DN constant. .

Simplifying the above leads to a direct connection from the partial sums of the MRB constant series and Foias' 2nd constant Both constructed at the turn of the millennium.

The MRB constant foundations

Weinstein, Eric W.PHD, published a continued fraction due to Khovanskii (1963)

yielding an infinite alternating sum of a continued fraction of polynomials that evaluates the MRB constant (CMRB) from axioma.

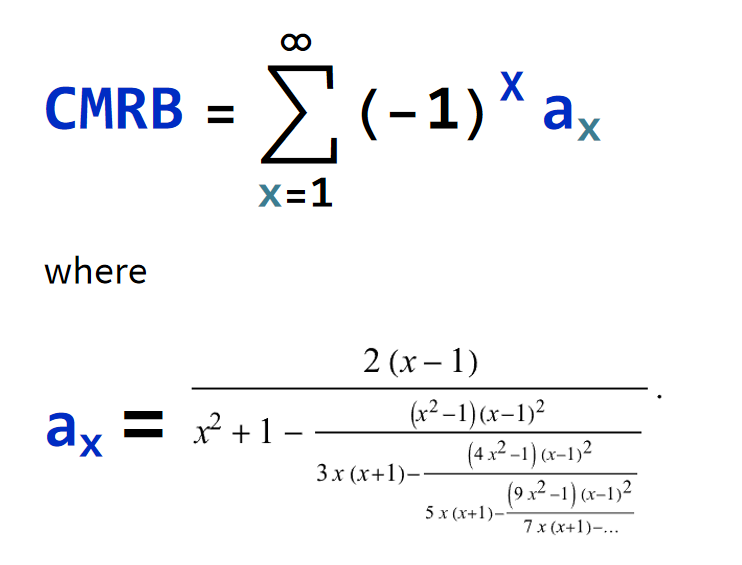
Like a "self-evident abacus" of sorts, this generalized continued fraction series axionically generates digits of the MRB constant.

Evaluate the series by defining addition $S(a+b)$ and through the concept of iteration along with the additive inverse, we can proceed as follows:

1. Define Addition (S):

• We already have the operation defined as $S(a+b)$. This represents the sum of two numbers a and b. Let's assume we are working within the set of integers for now.

2. Define Successor (and implicitly, Predecessor):

• We can define the successor of a number n, denoted as succ(n), as S(n+1). This means adding 1 to n.
• Conversely, we can think of a predecessor, denoted as pred(n), as the number that when added to 1 gives n. For this we will use the concept of the additive inverse that will be defined in the subtraction section. If succ(x) = n, then pred(n) = x.

3. Define Iteration:

• Iteration is the repeated application of a function. We'll use it to define multiplication and exponentiation (if needed).
• We can denote the n-th iteration of a function f applied to a value x as fⁿ(x).
  • For example: f³(x) = f(f(f(x)))

4. (Needed Iteration for squaring) Define Multiplication (M):

• Multiplication can be defined as repeated addition.
• We can define multiplication of a and b (where b is a non-negative integer) recursively as follows:
  • M(a, 0) = 0 (multiplying by zero results in zero)
  • M(a, succ(b)) = S(M(a, b) + a) (multiplying a by the successor of b is equivalent to adding a to the result of multiplying a by b)

  Or, using iteration and the successor function: - M(a, b) can be viewed as applying the function f(x) = S(x + a) b times, starting with 0. So, M(a, b) = f<sup>b</sup>(0) where f(x) = S(x + a).

5. Define Subtraction (and Additive Inverse):

• Subtraction is the inverse operation of addition.
• We need the concept of the additive inverse: For every number a, there exists a number -a (its additive inverse) such that S(a + (-a)) = 0.
• We can define subtraction S'(a-b) as S(a + (-b)). That is, subtracting b from a is the same as adding the additive inverse of b to a.

• Finding the Additive Inverse (Negation):

  • To find the additive inverse of a positive integer a
    1. Start with x = 0.
    2. Repeatedly apply the pred() function to x.
    3. When we arrive to a state such that S(x+a) = 0, that x is the additive inverse of a.
  • For negative integers, the process would be done with the succ() function.

6. Define Division (D):

• Division can be defined as repeated subtraction.
• Let's define division of a by b (where b is a non-zero integer) as finding a quotient q and a remainder r such that a = M(b, q) + r and 0 <= r < |b| (where |b| is the absolute value of b).
• We can find q recursively:
  • If S(|a|-|b|) < 0, then q = 0 and r = a
  • Otherwise, D(a, b) = (S(q'+S(0+1)),r') where (q',r')=D(S(a-|b|),b). The sign of q depends on the sign of a and b.
    • If a and b have the same sign, the sign of q is positive.
    • If a and b have different signs, the sign of q is negative.

• Or, using iteration:

  • We could repeatedly subtract b (or -b if a is negative) from a until the result is less than |b|. The number of times we subtract is the quotient, and the remaining value is the remainder.
  • Similar to the recursion above, the sign of the quotient is determined by whether the dividend (a) and divisor (b) have the same sign (positive quotient) or different signs (negative quotient).

In summary:

By starting with addition and employing iteration, the concept of the successor/predecessor, and the additive inverse, we can build up all the definitions of multiplication (and squaring), subtraction, and division. This demonstrates how, through fundamental arithmetic operations, the generalized continued fraction series generates several digits of the MRB constant.

-The classification of the MRB constant

There exists an interesting situation with the MRB constant. The nature of this constant opens up several intriguing possibilities:

Is the MRB constant, the sum of only unrelated algebraic numbers, transcendental?

Transcendental: If the MRB constant were transcendental, it would not be the root of any non-zero polynomial equation with rational coefficients. Transcendental numbers, like π and e, have complex properties that make them unique in the field of mathematics.

If not, is the MRB constant, the sum of only unrelated irrational numbers, rational?

Rational vs. Irrational: If the MRB constant is the sum of unrelated irrational numbers, one might question whether it could be rational. However, if it cannot be expressed as the quotient of two integers, it remains irrational. Irrational numbers have non-repeating, non-terminating decimal expansions and cannot be represented as a simple fraction.

If the answers to both of those questions are no and no, then there exists an infinitude of unrelated digits that represent the MRB constant which satisfy a polynomial equation with integer coefficients.

Algebraic: If the MRB constant is neither transcendental nor a sum of unrelated irrational numbers that is rational, it might be algebraic. This would mean it satisfies a polynomial equation with integer coefficients, indicating a structured and potentially solvable nature.

The classification of the MRB constant as rational or irrational, and as transcendental or algebraic, presents a fascinating area of exploration. Each possibility carries with it implications for our understanding of number theory and the broader mathematical landscape.

- Precursors of the MRB constant

Though I first presented a constant as the alternating sum of the sequence of nth roots of the whole set of natural numbers at the setting of the millennium, the concept of summing roots of algebraic numbers has a long and rich history.

1 www.kylem.net

2 www.expii.com

3 link.springer.com

• As the MRB constant is the alternating sum of the real-valued nth roots of the sequence of natural numbers, reaching back all the way to 1926 a product of the real-valued nth roots of the sequence of natural numbers was found to be of great importance,

While stating,

If e^γ is a rational number, then its denominator must be greater than 10¹⁵⁰⁰⁰.

. Shockingly, Wikipedia mentions

[ it is the product of real numbered roots]

that possibly could be related to CMRB:

• Interestingly,

This reminds me of when one follower of this post asked are there a bunch of MRB constants:

The terms of the series

      first 100 terms of the series:*)  m100 = Table[N[(-1)^k (k^(1/k) - 1), 200], {k, 1, 100}]; <p>whose partial sums give raise

the the MRB constant (see for example in this community <a href="http://community.wolfram.com/groups/-/m/t/743474">Record breaking direct summation of MRB constant ) contain the k-th root of k.

As always the question about all the other roots in the complex plane comes up:

  Remove[burnsStrip]
 burnsStrip[k_?NumericQ, w_?NumericQ] := 
 Block[{m = RotationTransform[k, {-1, 0}]},
  Polygon[{m[{-5/2, -w}], m[{1/2, -w}], m[{1/2, w}], m[{-5/2, w}]}]
  ]

Graphics[{{Green, burnsStrip[0, 1/40]}, {Yellow, 
   Sequence @@ (burnsStrip[#, 
        1/40] & /@ (Degree {143.8, 120, 90, 60, 36.2}))}, 
  Table[Point /@ 
    Evaluate[
     ReIm[(-1)^k  ((Flatten[Evaluate[Block[{x}, Solve[x^k == k, x]]]])[[All, 2]] - 1)]], {k, 1, 217}]}, 
 Frame -> True, AspectRatio -> 3/4.7, PlotRange -> All, 
 PlotLabel -> "A Bunch Of Burns Constants"]

giving

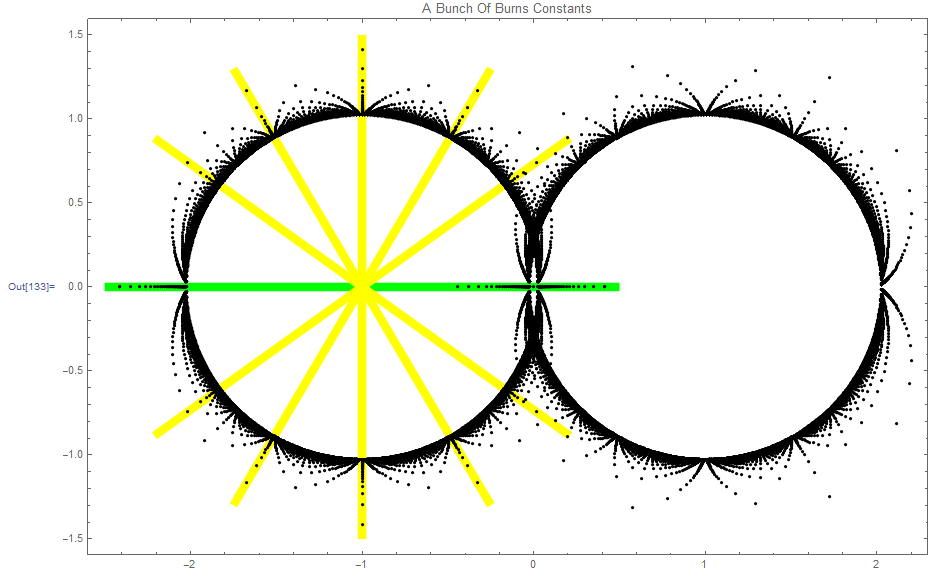
The terms for the MRB constant are in the green strip in the interval (-1/2,1/2). It is special, as the graphics shows clearly.

But is it sure, that the partial sums of terms on straight lines through -1 + 0 I or on straight lines through 1 + 0 I do all go to zero? Those (if any) which do not are satellites of the MRB constant.

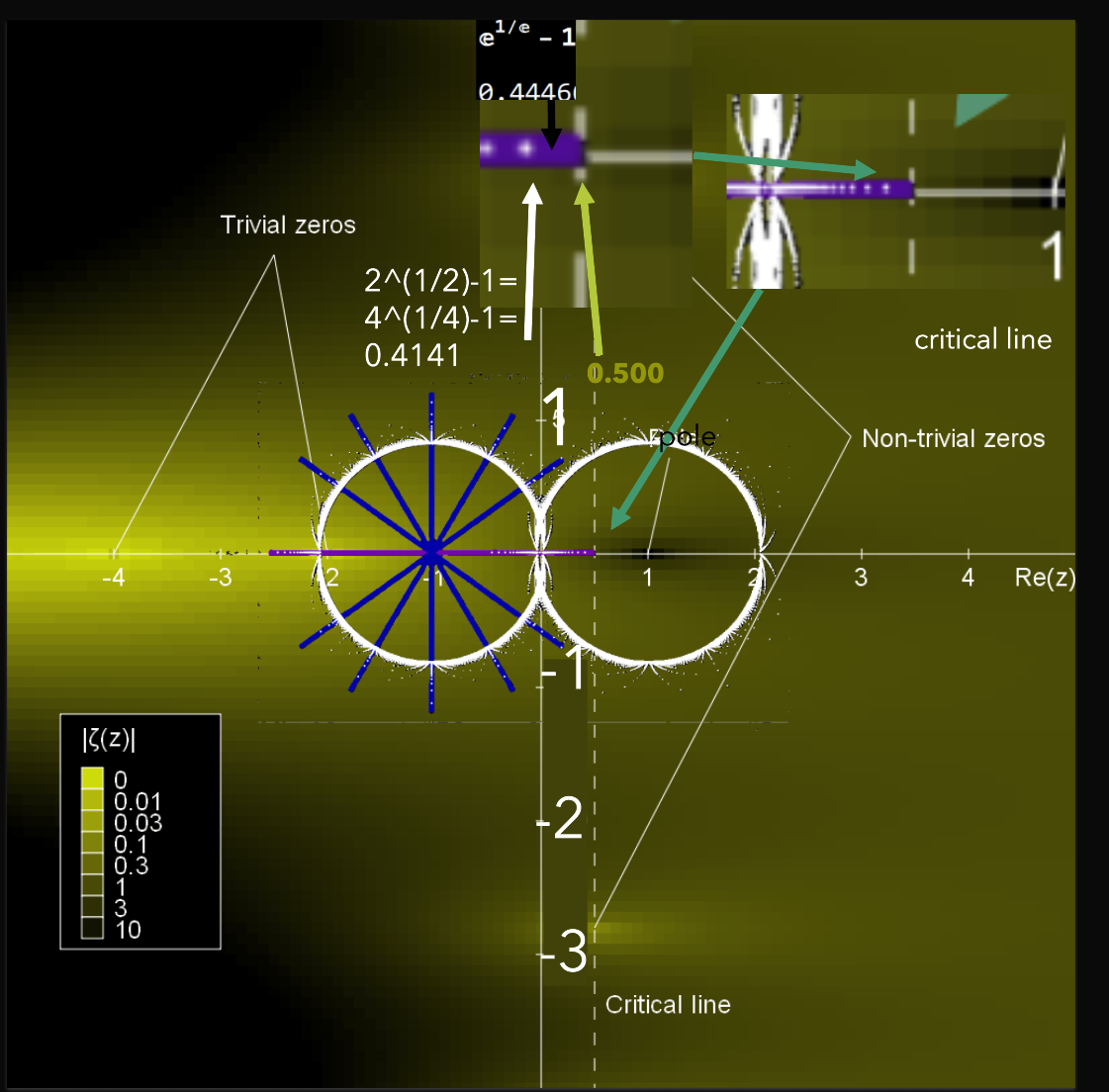
As presumed above, the Riemann Hypothesis determining the distribution of the nontrivial zeta zeroes has an indirect connection through the mathematical MRB construct to it.