Hello,

My goal is to define a multi-layer graph structure with some basics operations such as (Vertex/EdgeList, AdjacencyList, Edge/VertesCount, MultiGraphPlot...) in Mathematica/WolframLanguage.

A multi-layer graph (or multiplex graph) G(X, E1, E2, ..., EN) is defined by a single set of vertices X and multiple sets of edges (directed or not) E1, E2, ... EN.

Various representations may be used to represent such graphs:

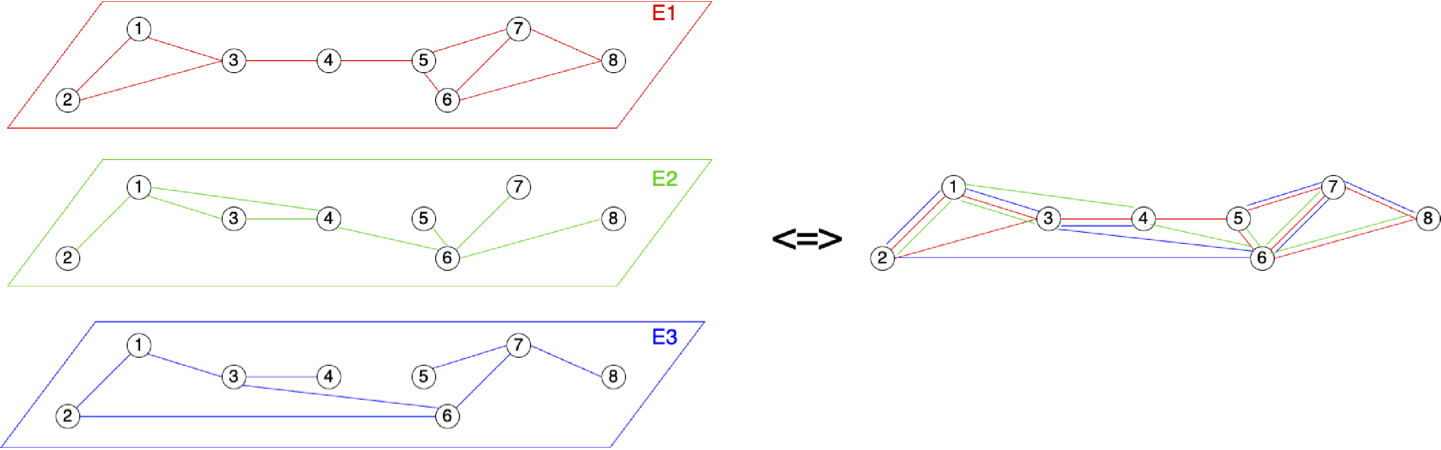On the left a representation using layers and on the right a projected view of the graph.

I have done few attempts I want to share with the community in the case I missed something or I get usefull advices.

To run the tests lets define a to toy dataset:

individuals = { 1, 2, 3};
friendWith = { 1 \[UndirectedEdge] 2};
workWith = { 1 \[UndirectedEdge] 2};

First attempt : Staying as closed as possible from the Graph function/primitive of the language:

First observation: Graph[...] supports multi-edges so we can have a graph with multiple edges linking two vertices if these two vertices are linked in multiple layers.

g = Graph[
     individuals,
     Join[
           friendWith,
           workWith
        ],
     VertexLabels -> "Name"
    ]

At this point we want to differenciate the edges according to the layer they are part of.

Mathematica allows edge labeling:

g = Graph[
     individuals,
     Join[
           Map[ Labeled[#, "friendWith"] &, friendWith],
           Map[ Labeled[#, "workWith"] &, workWith]
        ],
     VertexLabels -> "Name"
    ]

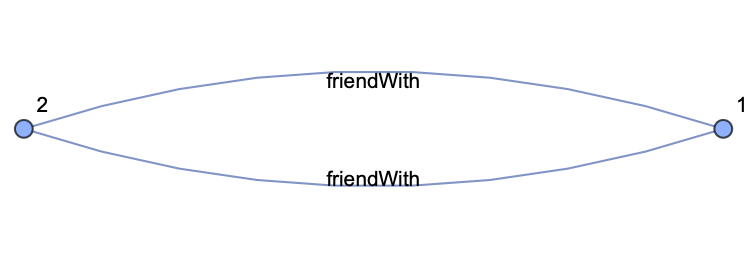
Unfortunately only the last labeling is stored. Mathematica seems to maintain a unique general list of the egde labels making impossible to differenciate them this way.

This option seems to be a dead way.

Second attempt : Defining a meta structure

An tedious alternative is to introduce a custom data structure like:

MutliGraph::usage="MutliGraph[ g1_Graph, g2_Graph, ..., gN_Graph] represents a multilayer graph";

And recoding the basics services we need:

EdgeLists[ graphs_MultiGraph ] := Map[ EdgeList, List @@ graphs ] ;
MultiGraph /: EdgeList[ graphs_MultiGraph ] := Join @@ EdgeLists[ graphs ] ;

VertexLists[ graphs_MultiGraph ] := Map[ VertexList, List @@ graphs ]
MultiGraph /: VertexList[ graphs_MultiGraph ] := Union @@ VertexLists[ graphs ] ;

AdjacencyLists[ graphs_MultiGraph ] := Map[ AdjacencyList, List @@ graphs ] ;
MultiGraph /: AdjacencyList[ graphs_MultiGraph ] := AdjacencyList @ Graph[ VertexList[ graphs ] , EdgeList[ graphs ] ] ;

EdgeCounts[ graphs_MultiGraph ] := Map[ EdgeCount, List @@ graphs ] ;
MultiGraph /: EdgeCount[ graphs_MultiGraph ] := Total @ EdgeCounts @ graphs ;

MultiGraph /: Subgraph[ graphs_MultiGraph, selection_ ] := Apply[ MultiGraph, Map[ Subgraph[ #, selection ] &, List @@ graphs ] ] ;

This second option do the job but is way less flexible.

I thank everyone reading this and I would be gratefull for any advice.

Regards,

Guillaume