The function Eigenvectors seems to generate different results every time, when using the method "FEAST" in version 10.

I have a hermitian matrix

H={{307.15,-0.185+0. I,-3.11835*10^-17-5.30092*10^-17 I,5.80793*10^-18-8.83487*10^-17 I,1.10548*10^-16-2.20872*10^-17 I},{-0.185+0. I,282.85,-0.185+0. I,-3.11835*10^-17-5.30092*10^-17 I,5.80793*10^-18-8.83487*10^-17 I},{-3.11835*10^-17+5.30092*10^-17 I,-0.185+0. I,259.55,-0.185+0. I,-3.11835*10^-17-5.30092*10^-17 I},{5.80793*10^-18+8.83487*10^-17 I,-3.11835*10^-17+5.30092*10^-17 I,-0.185+0. I,237.25,-0.185+0. I},{1.10548*10^-16+2.20872*10^-17 I,5.80793*10^-18+8.83487*10^-17 I,-3.11835*10^-17+5.30092*10^-17 I,-0.185+0. I,215.95}};

Conjugate[Transpose[H]] == H
(*True*)

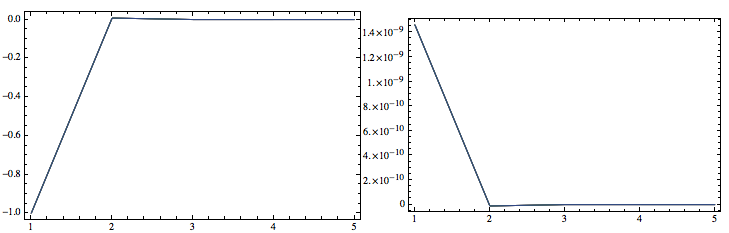
calculate the first eigenvector, repeat 5 times, plot the real and imaginary part

ls = Table[Eigenvectors[H, Method -> "FEAST"][[1]], {5}];

Row[{ListPlot[Re@ls, PlotRange -> {All, All}, ImageSize -> Medium], ListPlot[Im@ls, PlotRange -> {All, All}, ImageSize -> Medium]}]

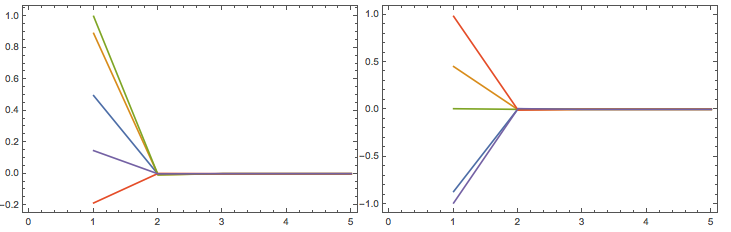
So why do I get different results? I have verified that those five different results are the correct eigenvectors for H, with only different phases, but I'm still wondering where does this kind of "randomness" come from, and how to avoid it.

As a comparison, I get the same results every time in version 9 when using the default method.