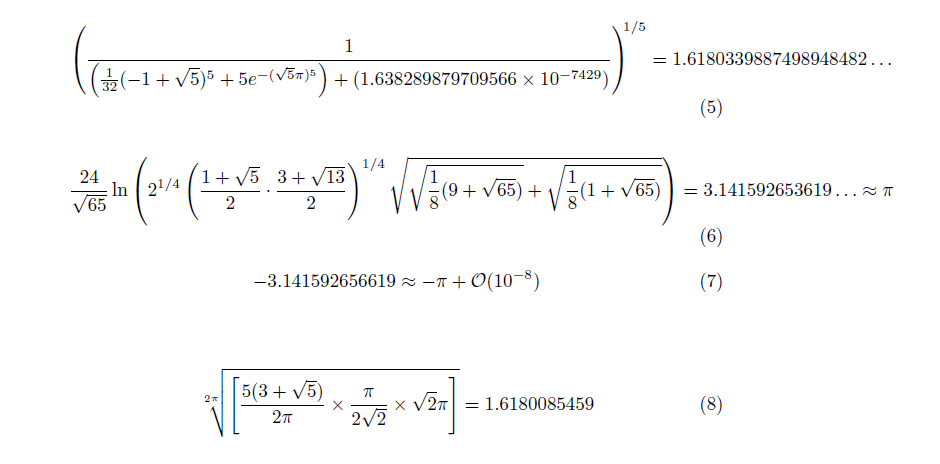Nardelli's Master Equation Complete Set

\begin{document}

d/dt (S * G) = Subscript[k,DN] * (integrate(exp(phi) * Subscript[G,A] * star(Subscript[G,A]), X) + (1/(4pi)) * integrate(tr(F^2) - tr(R^2), S/Subscript[Z,2])) + (3 * Subscript[k,DN] * Delta^2) /((2pi)^2 * Subscript[l,p]^2 * (r^2 + a^2)^2) =

\begin{equation} \boxed{=0.007357} \Rightarrow \left[\frac{1}{0.007357}\times13 - 21\right]^{1/16} + \frac{1}{8}C_{\text{MRB}} \end{equation}

\begin{equation} 1.617996 \approx \phi = \frac{\sqrt{5}+1}{2} = x^3-2x^2+1 \end{equation}

\begin{equation} \frac{\int_{M+r} d\rho\,\omega}{\|v(t)\|} \times \frac{1}{\|\rho(t)\|\|\rho(r)\|\|r(t)\|} = 1.6180065459 \end{equation}

\begin{equation} \left( \frac{1}{ \left( \frac{1}{32}(-1+\sqrt{5})^5 + 5e^{-(\sqrt{5}\pi)^5} \right) + (1.638289879709566 \times 10^{-7429}) }\right)^{1/5} = 1.6180339887498948482\ldots \end{equation}

\begin{equation} \frac{24}{\sqrt{65}}\ln\left(2^{1/4}\left(\frac{1+\sqrt{5}}{2}\cdot\frac{3+\sqrt{13}}{2}\right)^{1/4}\sqrt{\sqrt{\frac{1}{8}(9+\sqrt{65})} + \sqrt{\frac{1}{8}(1+\sqrt{65})}}\right) = 3.141592653619\ldots \approx \pi \end{equation}

\begin{equation} -3.141592656619 \approx -\pi + \mathcal{O}(10^{-8}) \end{equation}

\begin{equation} \sqrt[2\pi]{\left[ \frac{5(3+\sqrt{5})}{2\pi} \times \frac{\pi}{2\sqrt{2}} \times \sqrt{2}\pi \right]} = 1.6180085459 \end{equation}