I am trying to numerically solve a complex equation eq[x,y,μ] that includes a complex integral. The integrand contains the inverse hyperbolic tangent function ArcTanh[z] which gives real values for z<1 and complex values for z>1. My goal is to obtain the Re[y] and Im[y] roots of this equation as a function of the real parameter x for μ=2,5,10,100.

The exact solutions of this equation that I found in a book and which has three roots, are shown in Fig. 1 below:

• A real root y1>1: visible in the upper part of the Re[y] plot.
• A real root y2<0: which should be disregarded
• A complex root y3=Re[y3]+i Im[y3] (the one that is the most important): with 0<Re[y3]<1
  and Im[y3]<0

Fig.1 : Exact plots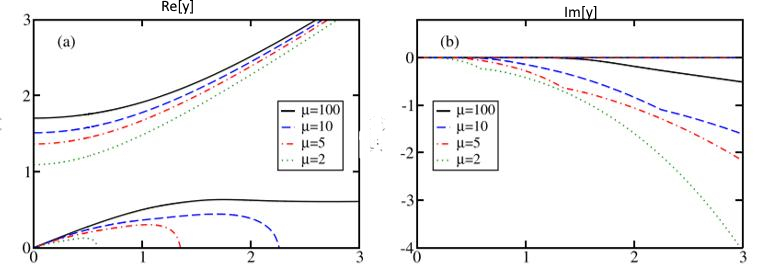

I have created the following Mathematica script, but I am unable to obtain the same plots. This discrepancy might stem from the initial estimates for the FindRoot or precision related issues in NIntegrate.

Clear["Global`*"]

(*------ Equation to solve ------*)
eq[x_,y_,\[Mu]_]:=1-x^2/y^2-((-1+y) \[Mu])/(2 x^2 y)-((1+y) \[Mu])/(2 x^2 y)+(\[Mu]^2 NIntegrate[ArcTanh[(x Sqrt[-1+s^2])/(s (y-1))] Exp[-\[Mu] s],{s,1,\[Infinity]},MaxRecursion->500])/(2 x y BesselK[2,\[Mu]])+((-x^2+(-1+y)^2) \[Mu]^2 NIntegrate[s^2 ArcTanh[(x Sqrt[-1+s^2])/(s (y-1))] Exp[-\[Mu] s],{s,1,\[Infinity]},MaxRecursion->500])/(2 x^3 y BesselK[2,\[Mu]])+(\[Mu]^2 NIntegrate[ArcTanh[(x Sqrt[-1+s^2])/(s (y+1))] Exp[-\[Mu] s],{s,1,\[Infinity]},MaxRecursion->500])/(2 x y BesselK[2,\[Mu]])+((-x^2+(1+y)^2) \[Mu]^2 NIntegrate[s^2 ArcTanh[(x Sqrt[-1+s^2])/(s (y+1))] Exp[-\[Mu] s],{s,1,\[Infinity]},MaxRecursion->500])/(2 x^3 y BesselK[2,\[Mu]])

(*------ Roots to calculate ------*)
rooty[x_?NumericQ,\[Mu]_?NumericQ]:=y/.FindRoot[1-x^2/y^2-((-1+y) \[Mu])/(2 x^2 y)-((1+y) \[Mu])/(2 x^2 y)+(\[Mu]^2 NIntegrate[ArcTanh[(x Sqrt[-1+s^2])/(s (y-1))] Exp[-\[Mu] s],{s,1,\[Infinity]},MaxRecursion->500])/(2 x y BesselK[2,\[Mu]])+((-x^2+(-1+y)^2) \[Mu]^2 NIntegrate[s^2 ArcTanh[(x Sqrt[-1+s^2])/(s (y-1))] Exp[-\[Mu] s],{s,1,\[Infinity]},MaxRecursion->500])/(2 x^3 y BesselK[2,\[Mu]])+(\[Mu]^2 NIntegrate[ArcTanh[(x Sqrt[-1+s^2])/(s (y+1))] Exp[-\[Mu] s],{s,1,\[Infinity]},MaxRecursion->500])/(2 x y BesselK[2,\[Mu]])+((-x^2+(1+y)^2) \[Mu]^2 NIntegrate[s^2 ArcTanh[(x Sqrt[-1+s^2])/(s (y+1))] Exp[-\[Mu] s],{s,1,\[Infinity]},MaxRecursion->500])/(2 x^3 y BesselK[2,\[Mu]])==0,{y,0.01-0.001I},MaxIterations->30,WorkingPrecision->20]

(*------ Re[y] and Im[y] Plots ------*)
ListLinePlot[Evaluate[{Table[{x,Re[rooty[x,100]]},{x,1/4,3,0.5}],Table[{x,Re[rooty[x,10]]},{x,1/4,3,0.5}],Table[{x,Re[rooty[x,5]]},{x,1/4,3,0.5}],Table[{x,Re[rooty[x,2]]},{x,1/4,3,0.5}]}],PlotRange->{{0,3},{0,3}},Frame->True,PlotRangePadding->0,GridLines->Automatic,GridLinesStyle->Directive[GrayLevel[0.8]],FrameStyle->Directive[13],Background->White,FrameLabel->{Text[Style["x",14]],Text[Style["Re[y]",14]]},PlotLegends->Placed[{"\[Mu] = 100","\[Mu] = 10","\[Mu] = 5","\[Mu] = 2"},{Scaled[{0.8,0.9}], {0, 0.7}}],ImageSize->450]

ListLinePlot[Evaluate[{Table[{x,Im[rooty[x,100]]},{x,1/4,3,0.5}],Table[{x,Im[rooty[x,10]]},{x,1/4,3,0.5}],Table[{x,Im[rooty[x,5]]},{x,1/4,3,0.5}],Table[{x,Im[rooty[x,2]]},{x,1/4,3,0.5}]}],PlotRange->{{0,3},{0.4,-4}},Frame->True,PlotRangePadding->0,GridLines->Automatic,GridLinesStyle->Directive[GrayLevel[0.8]],FrameStyle->Directive[13],Background->White,FrameLabel->{Text[Style["x",14]],Text[Style["Im[y]",14]]},PlotLegends->Placed[{"\[Mu] = 100","\[Mu] = 10","\[Mu] = 5","\[Mu] = 2"},{Scaled[{0.1,0.4}], {0.5, 0.7}}],ImageSize->450]

Here are my plots:

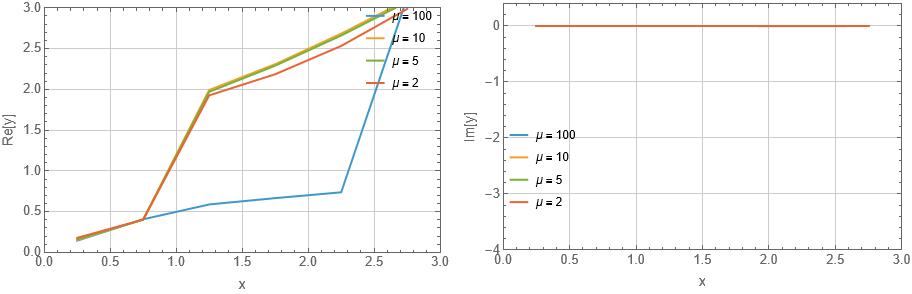
Any help in this regard would be deeply appreciated. Thanks in advance!