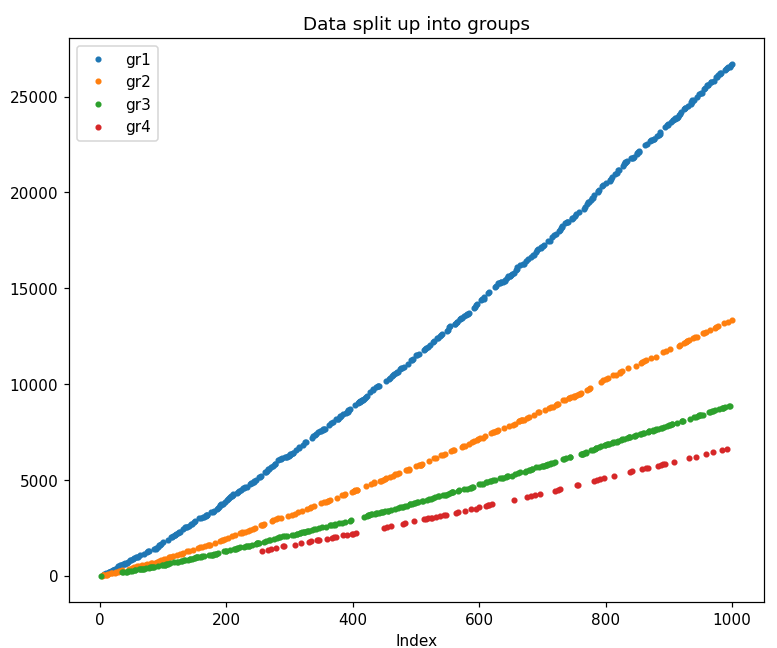
Would someone be able and willing to help to address the problem (which is reverse to the approximation solution described in one of the answers to https://math.stackexchange.com/questions/5030561 question) by writing the program, which will create four files for the four groups, containing in total 1000 OEIS A223881 prime numbers terms, where terms in the each group are prime numbers found just by using approximation formula y = C ∗ x^m, where "y" is the function real number value (which is the closest value to some prime in the OEIS A223881) for the integer argument "x", iterated from 1 to 1000, "m"- is the slope (all four curves have the same slope: m=1.197311990); "C" gives the displacement for the each of the curve. C1 =6.86845 C2 =3.420580 C3 =2.28335 C4 =1.70460 It appears to me that coding such a program is not a trivial task both mathematically and programmatically and is beyond my skills in those areas...

Here is my trial

m = 1.197311990;
cList = {6.86845, 3.420580, 2.28335, 1.70460};
xMax = 1000;

findClosestPrime[y_] := Module[{i = 0, lo, hi},
  While[True,
   lo = Floor[y - i];
   hi = Ceiling[y + i];
   If[lo >= 2 && PrimeQ[lo], Return[lo]];
   If[PrimeQ[hi], Return[hi]];
   i++
  ]
];

groupPrimes = Table[{}, {4}];
groupXs = Table[{}, {4}];

Do[
  results = Table[
    Module[{val = cList[[i]]*x^m, p, d},
     p = findClosestPrime[val];
     d = Abs[val - p];
     {d, i, p}
    ],
    {i, 4}
  ];
  best = MinimalBy[results, First][[1]];
  group = best[[2]];
  prime = best[[3]];
  groupPrimes[[group]] = Append[groupPrimes[[group]], prime];
  groupXs[[group]] = Append[groupXs[[group]], x];
  ,
  {x, 1, xMax}
];

validation = Table[
   And @@ Table[
     Abs[cList[[i]]*groupXs[[i]][[k]]^m - groupPrimes[[i]][[k]]] < 0.5,
     {k, Length[groupPrimes[[i]]]}
   ],
   {i, 4}
];

<|"GroupCounts" -> Length /@ groupPrimes, "Validation" -> validation|>