I tried to cut a Г-shaped hole inside a rectangle but got different results depending on whether a primitive was wrapped as a Region or passed directly. According to the documentation, both approaches—applying RegionDifference or RegionUnion to regions or graphics primitives—should behave the same.

Example

Path 1: Using Graphics Primitives Directly

outer = RegionDifference[
  Rectangle[{-1, -1}, {1, 1}],
  RegionUnion[
    Rectangle[{-0.9, -0.9}, {0.9, -0.4}],
    Rectangle[{0.4, -0.9}, {0.9, 0.4}]
  ]
];

outer

This returns:

Polygon[{{-1., 1.}, {1., 1.}, {1., -1.}, {-1., -1.}} -> {{{0.4, -0.9}, {0.9, -0.9}, {0.9, -0.4}, {0.9, 0.4}, {0.4, 0.4}, {0.4, -0.4}, {-0.9, -0.4}, {-0.9, -0.9}}}]

When plotted with Graphics:

Graphics[outer]

However, converting this to a Region and using RegionPlot:

RegionPlot[outer // Region]

Produces just a line (could it be, that Region ignores origin position?):

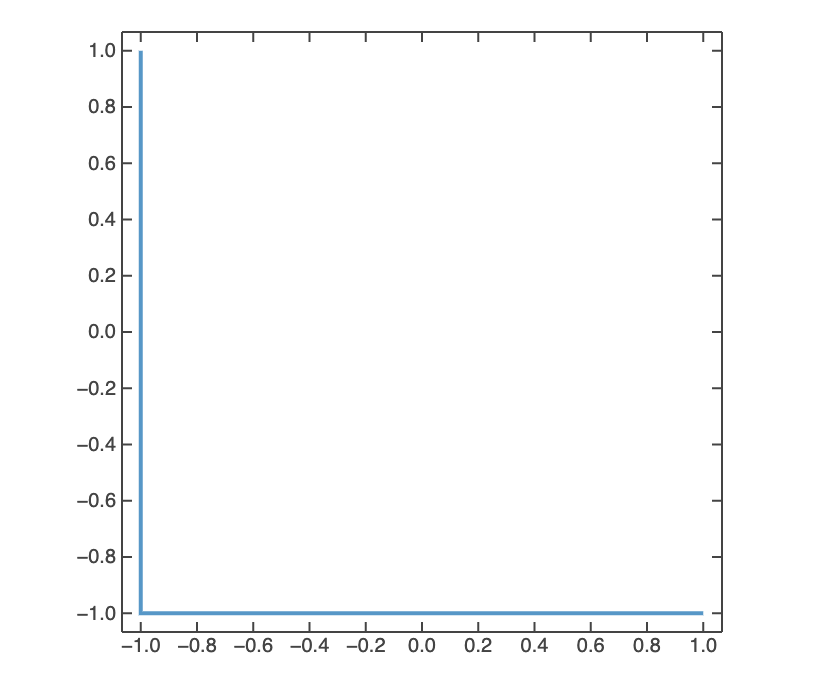
Path 2: Using Region on All Primitives

outer = RegionDifference[
  Rectangle[{-1, -1}, {1, 1}] // Region,
  RegionUnion[
    Rectangle[{-0.9, -0.9}, {0.9, -0.4}] // Region,
    Rectangle[{0.4, -0.9}, {0.9, 0.4}] // Region
  ]
];

RegionPlot[outer]

This gives the same thin line:

Thanks.

UPD: I checked my region with a test point, it returns incorrect results

RegionMember[outer, {0, 0}]

False