Hi dear community, I have a question about the automatic recognition of boundary regions on which conditions are imposed and the discretization and solution with finite elements. Consider the example in the Mathematica documentation

Needs["NDSolve`FEM`"]
Region = ImplicitRegion[Not[(x - 5)^2 + (y - 5)^2 <= 3^2], {{x, 0, 5}, {y, 0, 10}}];
op = -Laplacian[u[x, y], {x, y}] - 20;
BCs = {DirichletCondition[u[x, y] == 0, x == 0 && 8 <= y <= 10],DirichletCondition[u[x, y] == 100, (x - 5)^2 + (y - 5)^2 == 3^2]};
uif = NDSolveValue[{op == 0, BCs}, u, Element[{x, y}, Region]];
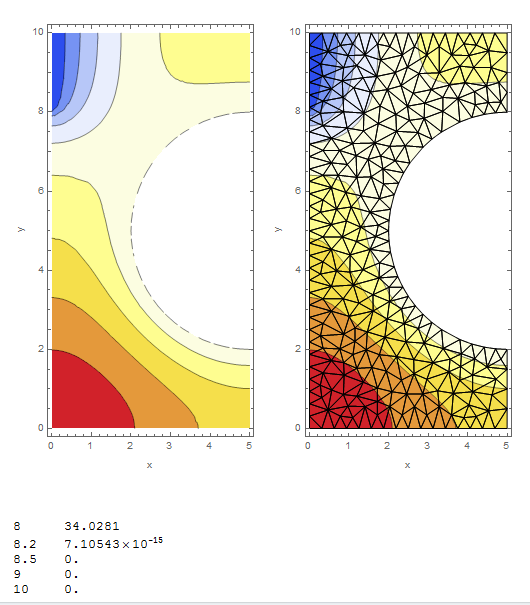
plot = ContourPlot[uif[x, y], Element[{x, y}, Region],ColorFunction -> "Temperature", AspectRatio -> Automatic,FrameLabel -> {"x", "y"}];
mesh = uif["ElementMesh"];
GraphicsRow[{plot, Show[plot, mesh["Wireframe"]]}, ImageSize -> 500]
bvals = Table[{y, uif[0, y]}, {y, {8, 8.2, 8.5, 9, 10}}] // TableForm

(See output as image at the bottom)

My problem are the boundary values "bvals" computed from the FE-solution "uif" at x=0 and y = {8,8.2,8.5,9,10}. In the given boundary conditions "BCs" of the function u shoulg ave the value 0 at x=0 and y in 8,10. Due to the automatic mesh generation (see output image) the nodes do NOT include exactly the point x=0 and y=8 (see output bvals, at x=0, y=8 you get the value 34 instead of 0 as imposed in the BCs). Are there thoughts of the Mathematica developers to automatically detect exact points on the boundary which belong to the boundary conditions? I am sure it is possible to do this by first creating a boundary mesh manually but I think that this should be automatically done per default. Any suggestions for the mean time to do this? Thank you very much

Mauricio