Group Abstract Group Abstract

Message Boards Message Boards

0
|
271 Views
|
4 Replies
|
4 Total Likes
View groups...
Share
Share this post:

Ordering four points into a closed quadrilateral with Wolfram

Jim Clinton
Posted 3 days ago 
pts = {{0, 0}, {1, -1}, {1, 1}, {4, 0}}

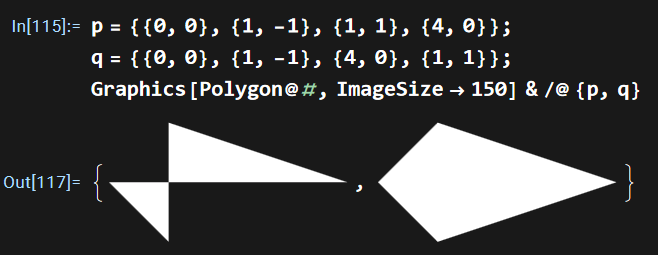
enter image description here

How to use Mathematica code to reorder the coordinates of any four given points so that they are arranged (either clockwise or counterclockwise) as the four points of a closed quadrilateral as follows and so on. The polygon drawn with the reordered coordinates is shown in the right-hand panel above.

{{0, 0}, {1, -1}, {4, 0}, {1, 1}}

Or

{{1, -1}, {4, 0}, {1, 1}, {0, 0}}

Or

{{4, 0}, {1, 1}, {0, 0}, {1, -1}}

Extending the above problem: suppose we are given n arbitrarily ordered points that are known to form a simple closed n-gon; how can we reorder them—clockwise or counter-clockwise—so that the list can be used to plot the polygon correctly and compute its area?The purpose is to make the code universal.
POSTED BY: Jim Clinton
4 Replies
Sort By:

There can be more than one reordering that makes a simple closed polygon. Here is my attempt:

properIntersection[{Line[pts1_], Line[pts2_]}] := 
 RegionDifference[RegionIntersection[Line[pts1], Line[pts2]], 
  Point[Join[pts1, pts2]]];
notSelfIntersectsQ[pts_?MatrixQ] := 
  RegionUnion @@ 
    Map[properIntersection, 
     Subsets[Map[Line, Partition[pts, 2, 1, {1, 1}]], {2}]] == 
   EmptyRegion[2];
findSimplePolygons[pts_?MatrixQ] := 
  Select[Map[Prepend[pts[[1]]], Permutations[Rest[pts]]], 
   notSelfIntersectsQ];
pts = {{0, 0}, {2, -3}, {1, -1}, {1, 1}, {4, 0}};
Graphics[Point[pts]]
reorderings = 
 findSimplePolygons[{{0, 0}, {2, -3}, {1, -1}, {1, 1}, {4, 0}}]
Map[Graphics@*Polygon, reorderings]
POSTED BY: Gianluca Gorni
Hans Milton
Hans Milton
Posted 2 days ago

But there is only one reordering (CW or CCW) that maximizes the circumscribed area
POSTED BY: Hans Milton
Hans Milton
Hans Milton
Posted 2 days ago

You could use FindShortestTour
POSTED BY: Hans Milton
Eric Rimbey
Eric Rimbey
Posted 3 days ago

If you can assume that the polygons should be convex, then you can use a convex hull.

MeshPrimitives[ConvexHullMesh[pts], 2] // InputForm
(* {Polygon[{{0, 0}, {1, -1}, {4, 0}, {1, 1}}]} *)
POSTED BY: Eric Rimbey
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard