This year, the Nobel Prize in Physics was awarded to John Clarke, Michel H. Devoret, and John M. Martinis
"for the discovery of macroscopic quantum mechanical tunnelling and energy quantisation in an electric circuit".
nobelprize.org/prizes/physics/2025/summary
When I first read the citation, the only words that resonated with me were "electric circuits."
As an engineer, that was something familiar—but macroscopic quantum tunnelling? That sounded mysterious.
So, I decided to explore what it really means—by modeling it, simulating it, and connecting it back to engineering intuition.
Some background...
From Classical Mechanics to Quantum Tunnelling
When you throw a ball at a wall, it bounces back. It never appears on the other side.
But at the atomic scale, particles can tunnel through barriers they shouldn't be able to cross. This is what made quantum mechanics famous for being bizarre yet real. 
The Schrödinger equation (1926) predicts this behavior— the particle's wavefunction "leaks" into forbidden regions, giving a finite probability of finding it beyond the barrier.
Early Applications: Radioactive Decay and Fusion
Quantum tunnelling first explained alpha decay—how alpha particles escape the nucleus. It also revealed why decay is probabilistic: the rate depends on the barrier height and thickness.
As summarized by the Nobel committee:
"Tunnelling is also necessary for fusion to occur in our Sun, where the temperature and pressure are too low to classically allow two protons to overcome Coulomb repulsion and form a helium nucleus."
From Atoms to Superconductors
In the 1950s, Bardeen, Cooper, and Schrieffer formulated the BCS theory of superconductivity (Nobel 1972).
They showed that electrons can pair up into Cooper pairs, forming a collective quantum state that moves without resistance—a superfluid of electrons.
It's like fluid flow with zero viscosity: perfectly lossless.
The Josephson Prediction (1962)
Brian Josephson, then a graduate student, predicted that Cooper pairs could tunnel across a thin insulating barrier between two superconductors—even with no voltage applied.
This means a supercurrent can flow purely due to phase difference between superconductors despite being separated by an insulating barrier.
The effect was confirmed experimentally in 1963 and led to SQUIDs (Superconducting Quantum Interference Devices), used for ultra-precise magnetic sensing.
That theoretical leap—showing that quantum tunnelling can appear in an ordinary-looking circuit—laid the groundwork for this year's Nobel Prize.
Modeling & Simulation
The Current-Biased Josephson Junction
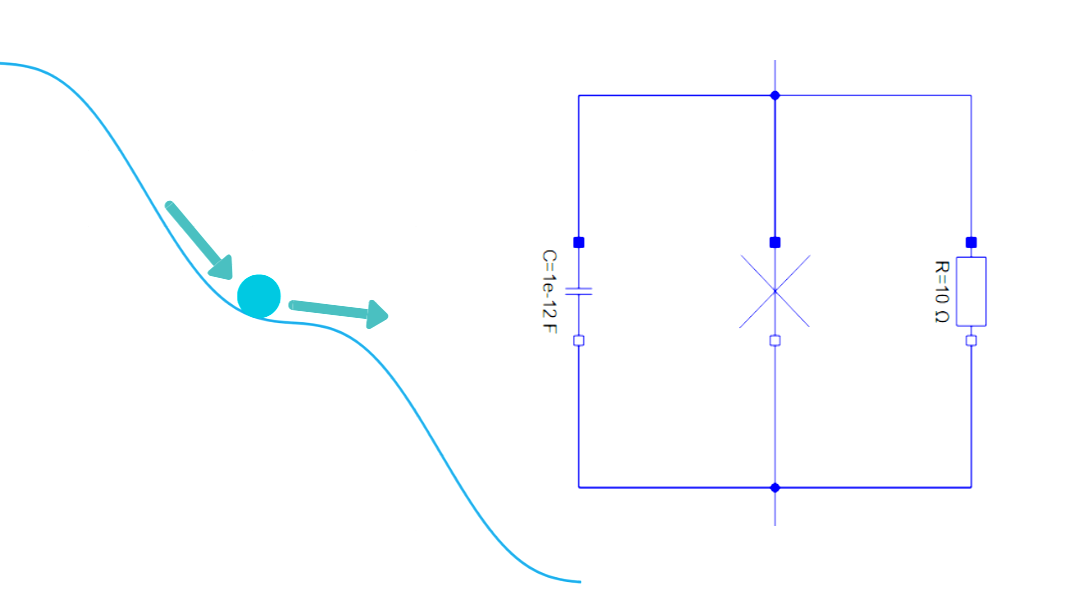
A Josephson junction is a simple device: two superconductors separated by an insulating barrier. 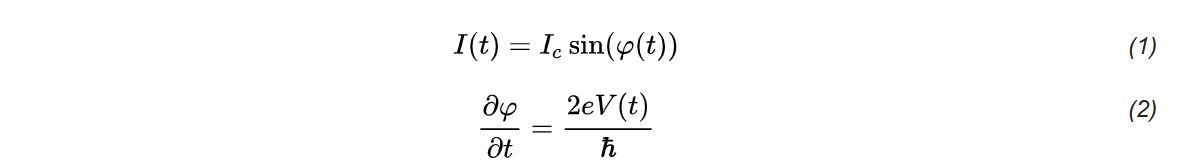
Equation (1) is called the first Josephson relation or weak-link current-phase relation, and equation (2) is called the second Josephson relation or superconducting phase evolution equation.
In circuit terms, it behaves like a nonlinear inductor with some capacitance and damping resistance. 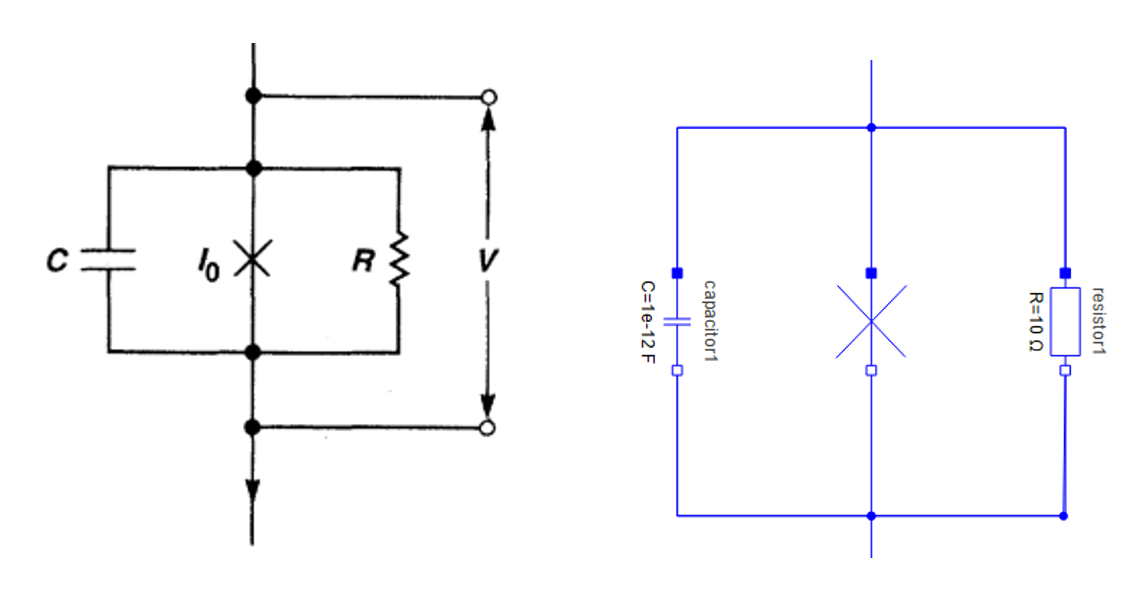
On left you see the schematics of the Josephson junction and on the right is a model in Wolfram System Modeler (a Modelica language based tool).
You can read more about the equations involved by reading the following paper (especially the section on "The current-biased Josephson junction")
https://www.nobelprize.org/uploads/2025/10/advanced-physicsprize2025.pdf
To understand the characteristics of the Josephson junction, we have connected it to a current source that produces the bias current. 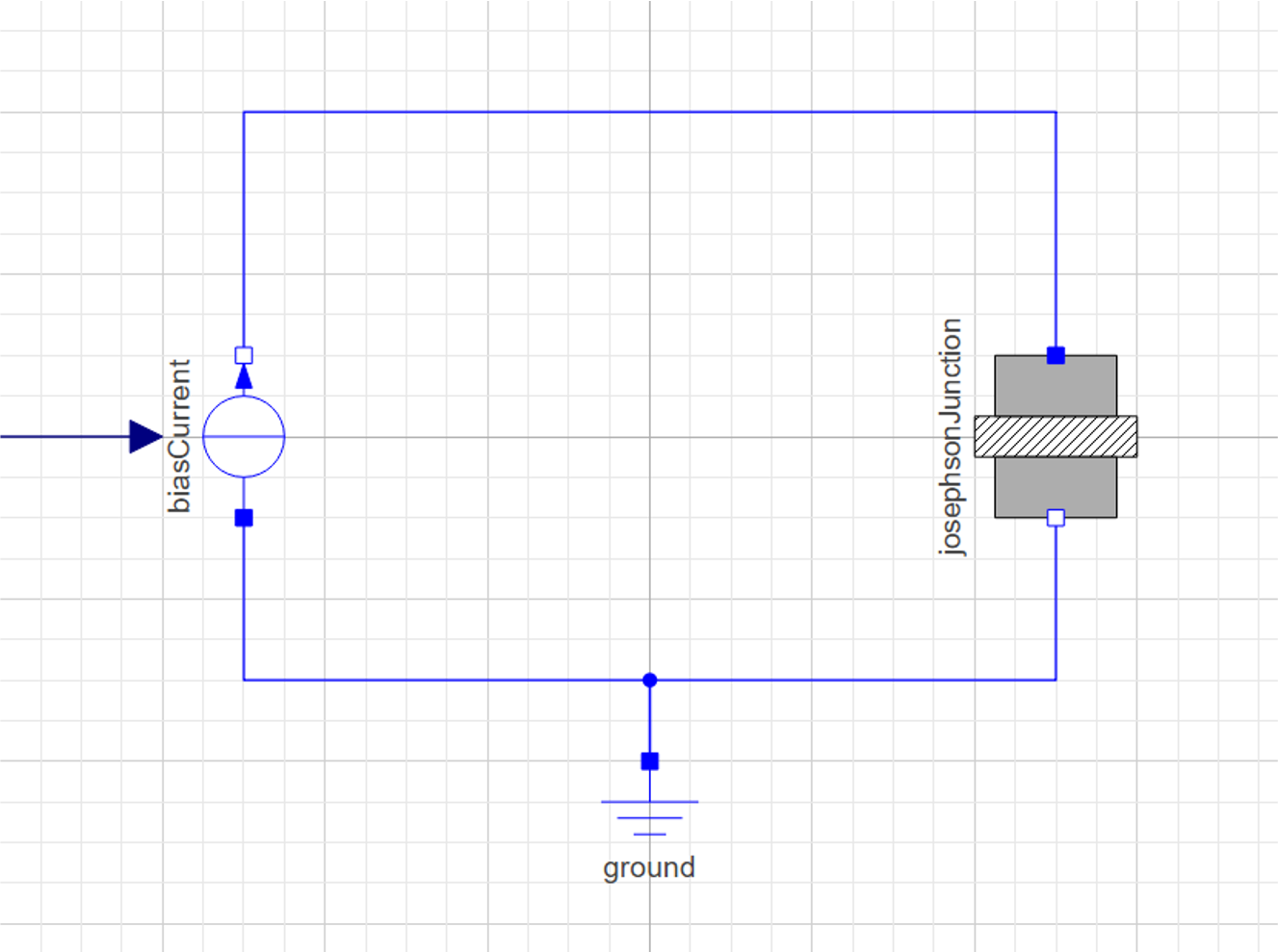
Understanding Key Characteristics
A Josephson junction is characterized by a parameter called critical current. Let's observe the behavior for three different bias currents.
- Bias current < Critical current
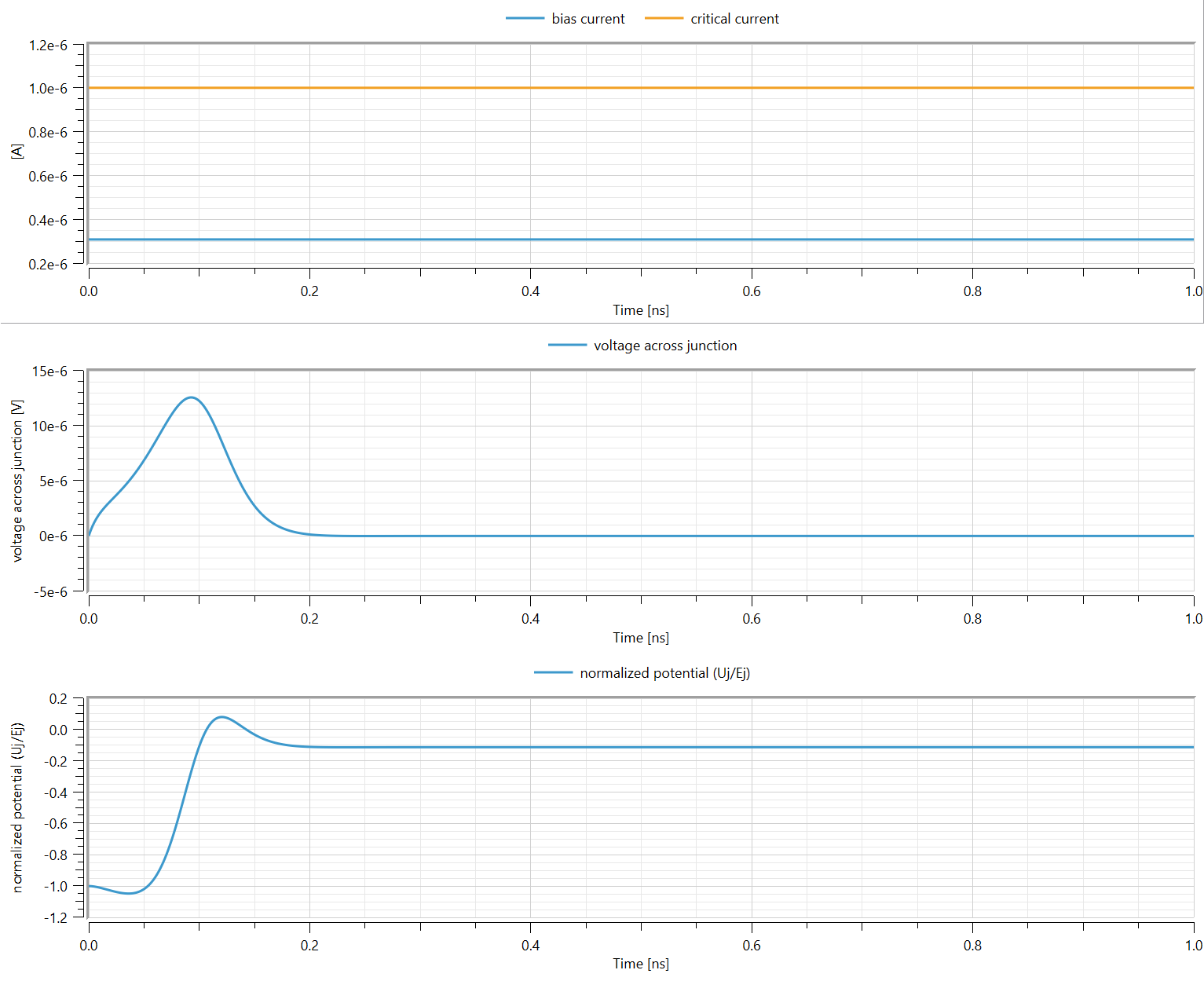
The phase "particle" sits in a well: The voltage drop across the junction settles to around 0 and the energy potential is constant.
- Bias current > Critical current
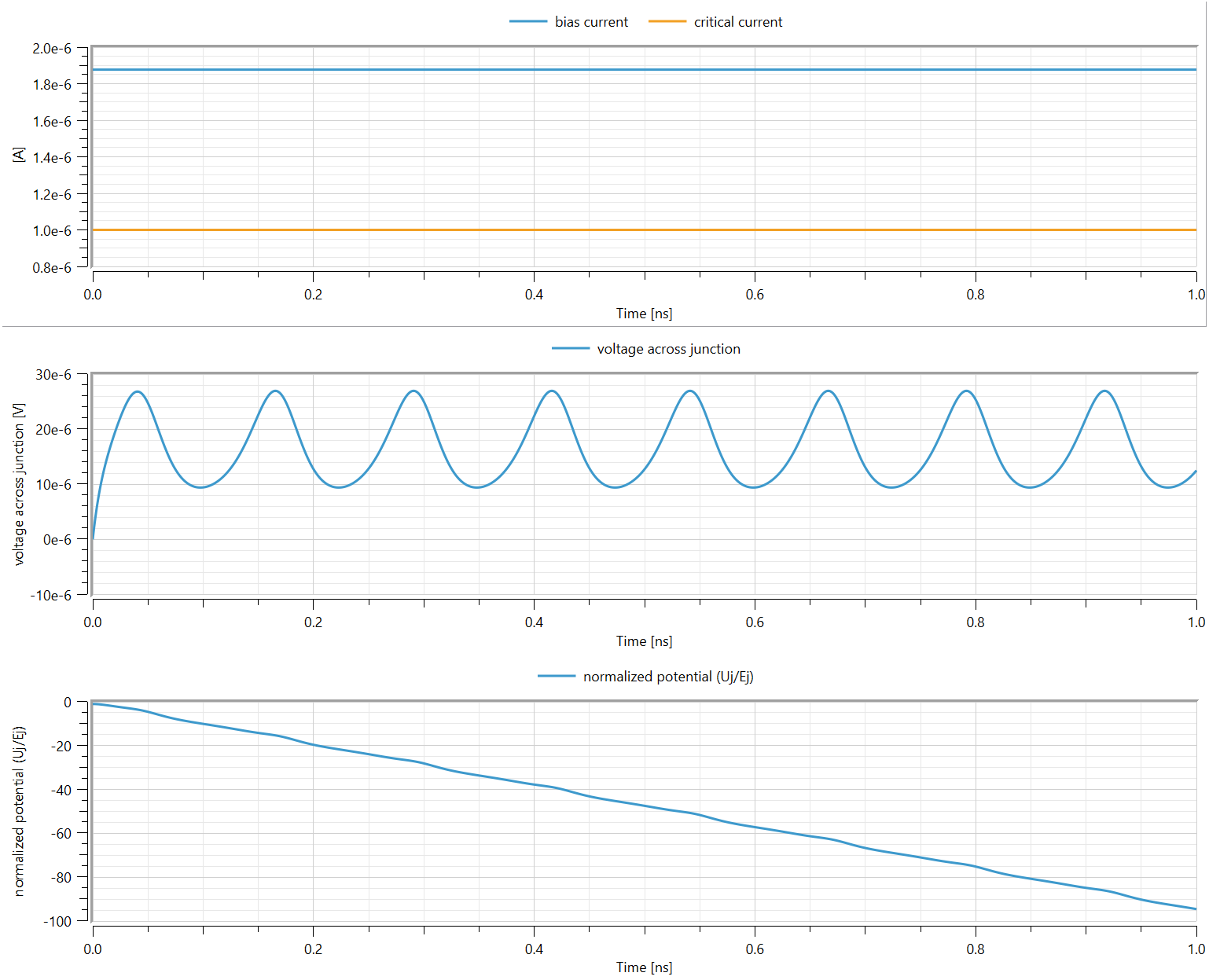
The particle rolls downhill: The junction is in a resistive state, represented by the non-zero voltage drop across the junction. The energy potential continuously decreases.
- Bias current is around the Critical current
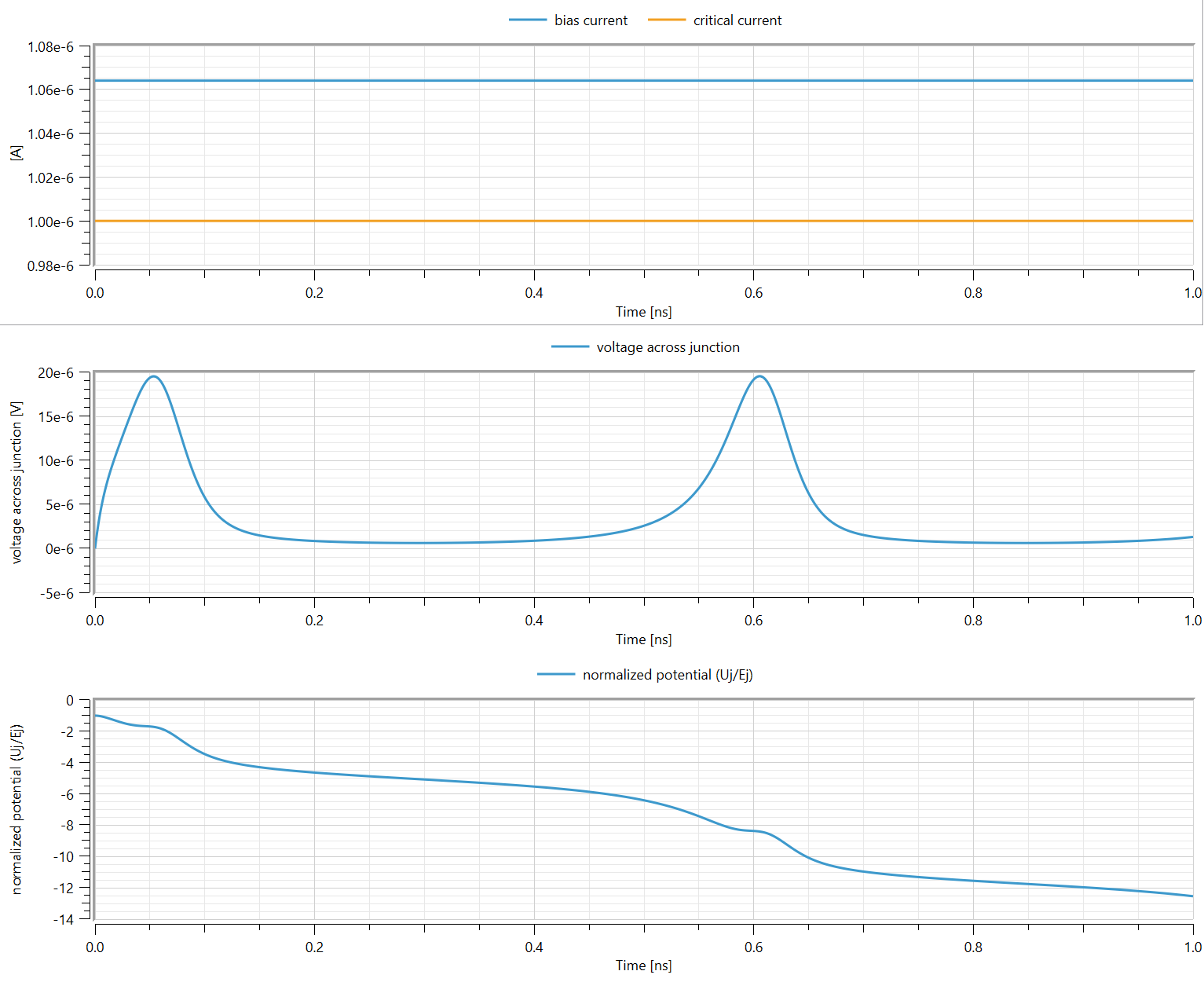
Occasional escapes from wells (Quantum tunnelling regime): The junction is usually superconducting (voltage drop around 0), but occasionally becomes resistive, and the energy potential drops. The occasional escapes can be thermally activated.
Understanding Energy Landscape—The Tilted Washboard
One of the interesting characteristics to observe in this model the potential energy stored in the junction. 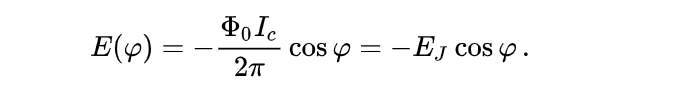
Visually, the potential looks like a washboard potential.
Let's compare it with the figure presented in the Nobel Committee report: 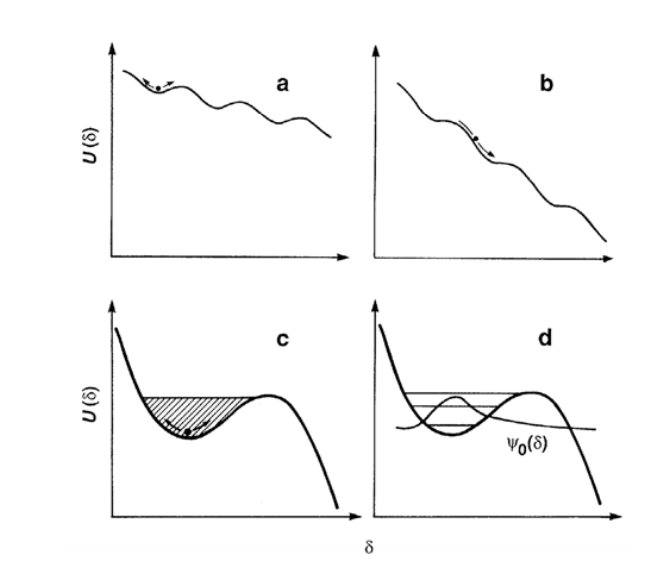
At zero temperature, a classical particle would stay forever in one well, but a quantum system can tunnel out, leading to macroscopic quantum tunnelling (MQT)—the phenomenon recognized by this year's Nobel Prize.
Advantages of Lumped Modeling
The modeling that I showed above is a lumped model. Lumped-element modeling enables engineers to represent quantum circuits—comprising Josephson junctions, capacitors, and inductors—as networks of nonlinear circuit elements that obey the same physical laws as classical RLC systems.
By formulating these as differential equations (e.g., RCSJ model), one can simulate the voltage, current, and phase dynamics to predict energy levels and coupling between qubits. This approach enables intuitive circuit-level design and parameter tuning before moving to full quantum or electromagnetic simulations.
From Models to Modern Technology
These equations underpin a vast range of modern technologies:
- Quantum computers—Superconducting qubits (transmon, flux, phase qubits) use Josephson junctions as tunable nonlinear inductors.
- SQUID magnetometers—Detect magnetic fields down to femtotesla levels.
- Quantum amplifiers—Low-noise amplifiers for qubit readout and deep-space communications.
- Voltage standards—Arrays of Josephson junctions define the volt via the Josephson constant.
The same "washboard" dynamics that I simulated in System Modeler are what experimentalists fine-tune at milli-Kelvin temperatures to design qubits and sensors.
Chronology of Key Discoveries
- 1933: Erwin Schrödinger: Quantum wave equation; tunnelling concept
- 1957—1972: Bardeen, Cooper, Schrieffer: BCS theory: superconductivity & Cooper pairs
- 1962—1973: Brian Josephson, Esaki, Giaever: Quantum tunnelling in superconductors
- 1980s—1990s: John Clarke, Michel Devoret: Observation of macroscopic quantum tunnelling
- 2000s—2020s: John Martinis & teams: Superconducting qubits and quantum circuits
- 2025: Clarke, Devoret, Martinis: Quantised energy levels in circuits
Further Reading
Scientific background from the Nobel Committee: https://www.nobelprize.org/prizes/physics/2025/advanced-information/
 Attachments:
Attachments: