Greetings to all you good folks of Mathematica!!

I'm still pretty new to Mathematica (only worked with it for about a month or so), so I would like to seek the advice of you guys regarding a geometrical problem.

Essentially, I need to find the volume of an ellipsoid that's bounded by a single inclined plane. This plane has to intersect the 'mid-point' of the outer edge of the ellipse at an angle. I know this is somewhat confusing (even to myself), but to illustrate what I mean, please have a look at the figure below:

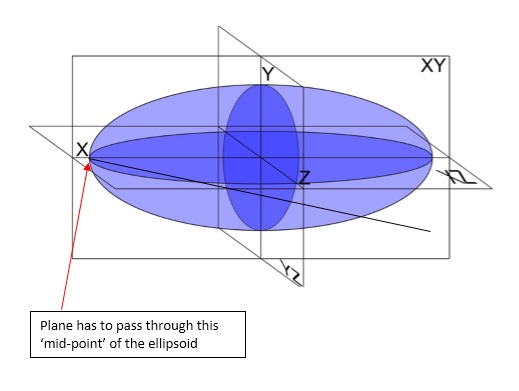
Basically, the plane would be the plane of XZ rotated clockwise about the pivot point of X.

I'm hoping this explains the problem better.

From there then, I need to find the volume of the ellipsoid underneath that plane. See the 2-D representation below:

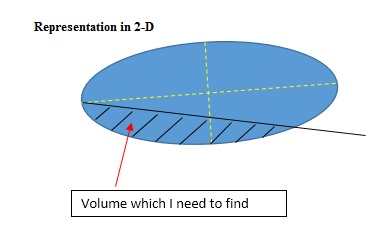
I've written the ellipsoid equation to obtain the volume, but I have a huge problem in trying to define that plane as an extra condition.

In[1]:= reg=ImplicitRegion[x^2/a^2+y^2/b^2+z^2/c^2<=1 && z<=0, {z, y, x}];

In[2]:= Volume[reg, Assumptions->a>0 && b>0 && c>0]

Anyone got any ideas?

Would really appreciate any advice from you guys.

Thank you.

Regards Corse