Further MRB constant Exploration
MRB constant Conditional Convergence

According to the Wolfram Notebook Assistant, the Riemann Series Theorem says:
By a suitable rearrangement of terms, a conditionally convergent series may be made to converge to any desired value, or to diverge.
According to the Wolfram Notebook Assistant, this may be done by:
(1.) Rearrange Positive and Negative Terms:
(2.) Target Sum:
Let S be the target sum you want the rearranged series to converge to.
(3.) Construct the Rearrangement:
- Start summing positive terms until the partial sum exceeds S.
- Add negative terms until the sum falls below S.
- Repeat this process, adding positive terms to exceed S, then negative terms to fall below S.
(4.) Convergence to S:
- This process constructs a new series that converges to S.
- Since both positive and negative sums diverge and can be made arbitrarily large, the partial sums can be made to oscillate around S and eventually converge to it.
Generalization:
By choosing different strategies for rearranging the terms, you can make the series converge to any real number or diverge.
This theorem shows the delicate nature of convergence in conditionally convergent series and the non-uniqueness of their sum under rearrangement.
For example,
$$ S = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots $$
converges to
$\ln 2$, but the same series can be rearranged to
$$ 1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{3} + \frac{1}{6} + \frac{1}{5} + \frac{1}{8} - \cdots $$
so the series now converges to half of itself.
The wonderful point of theorems is that they are true without exceptions. Hence, the MRB constant series of irrational terms must also equal any rational, as well as any transcendental number of our choosing! Despite an infinitude of them being irrational, as well as algebraic.
->Here<- is a rearrangement of terms of the MRB constant series that add up to within 6.48303*10^-7 of the value of pi.
MRB constant Absolute Convergence
an Analog to the Exponential Function
Leading to an Integral Representation
Below, analog-type- positioning of the MRB-constant and e-to-the x formulas stem from an absolutely convergent series.
Mathematica confirms it here:
In[405]:= test = (2 k)^(1/(2 k)) - (2 k + 1)^(1/(2 k + 1));
In[406]:= SumConvergence[Abs[test], k]
Out[406]= True
In mathematical analysis, series expansions provide powerful tools for approximating functions and exploring their properties. A classic example is the Taylor series expansion of the exponential function
$$e^x$$, which elegantly divides into sequences of even and odd powers. These sequences reveal deeper connections to the hyperbolic sine and cosine functions, where even powers correspond to the series expansion of
$$\cosh(x)$$ and odd powers to that of
$$\sinh(x)$$. This separation showcases the inherent symmetry and structure within the exponential function.
Similarly, the exploration of the MRB constant reveals intriguing parallels. The MRB constant is defined through an alternating series involving the expression
$$n^{1/n}$$. Just as with the exponential function, one can examine the series by segregating terms based on parity: odd versus even terms. This division, while not directly yielding trigonometric or hyperbolic functions, highlights a structural analogy that invites deeper investigation into the convergence and behavior of such series.
Both the decomposition of the exponential function and the partitioning of the MRB constant series into odd and even components underscore the rich interplay between algebraic expressions and their geometric or analytic interpretations. Understanding these connections enriches our comprehension of mathematical constants and functions, providing insights that extend beyond the immediate formulations.
When studying calculi of approximations as we do in this discussion, spectral analysis, or quantum field theories, replacing discrete sums, like the above MRB constant, with an integral involving hyperbolic functions can reveal deeper properties in such as
$$ \sum_{n=1}^{\infty} \left( \sqrt[2n]{2n} - \sqrt[2n-1]{2n-1} \right) ==
C_{MRB} = \int_{0}^{\infty} \frac{\mathfrak{F} \sqrt[1+t]{1+ i t}}{\sinh(\pi t)} dt .$$
The similarity in exponential decay or growth between discrete and continuous representations may explains the why of this equation.
Using a variation of the Abel–Plana formula:
$$\sum_{n=0}^\infty (-1)^nf(n)= \frac {1}{2} f(0)+i \int_0^\infty \frac{f(i t)-f(-i t)}{2\sinh(\pi t)} \, dt, $$
a follower going by the moniker Dark Malthorp presented a beautiful integral for the MRB constant, where for
\begin{equation*}
f(x) = 1 - (1 + i x)^{\frac{1}{1 + i x}}
\end{equation*}
$$C_{MRB}$$
$$== \sum_{0}^{\infty} \frac{\Re (f(t))}{\sinh(i \pi t)+\cosh(i \pi t)}$$
$$== \int_{0}^{\infty} \frac{\Im (f(t))}{\sinh(\pi t)} dt$$
To apply Abel-Plana, bounds on
$f(z)$ are needed. Although not holomorphic on
$\Re(z)$ at
$0$, it is still manageable since
$\lim_{x \rightarrow \infty} f(x + yi) = 0$ for all fixed
$y$, and it is bounded in the right half-plane. Using the alternating series formulation of Abel-Plana:
$$C_{MRB} = \sum_{n=0}^{\infty} (-1)^n f(n) = \frac{1}{2} f(0) + i \int_{0}^{\infty} \frac{f(it) - f(-it)}{2 \sinh(\pi t)} dt$$
relate the imaginary part terms to the MRB series\
Simplifying the integral:
\begin{align*}
&= \frac{1}{2} \cdot 0 + i \int_{0}^{\infty} \frac{1 - (1 + it)^{\frac{1}{1 + it}} - 1 + (1 - it)^{\frac{1}{1 - it}}}{2 \sinh(\pi t)} dt \
&= i \int_{0}^{\infty} \frac{-(1 + it)^{\frac{1}{1 + it}} + (1 - it)^{\frac{1}{1 - it}}}{2 \sinh(\pi t)} dt
\end{align*}
Holomorphic Property
Since
$(1 + \frac{1}{x})$ is holomorphic for
$\Re(z) \geq 0$ and real-valued for real
$z$, it follows that
$f(z) = \overline{f(z)}$. This leads to:
$$C_{MRB} = \int_{0}^{\infty} \frac{\Im (f(t))}{\sinh(\pi t)} dt $$
Although we cannot strictly pull the imaginary part out of the integral due to the pole at 0, the imaginary part remains bounded for
$t \in (0, \infty)$. I don't see why we cannot write
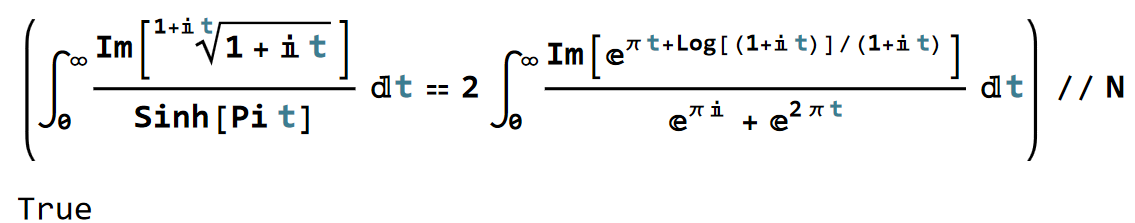 N[Integrate[
Im[(1 + It)^(1/(1 + It))]/Sinh[Pit], {t, 0, Infinity}] ==
2Integrate[
Im[E^(Pit + Log[1 + It]/(1 + It))]/(E^(PiI) + E^(2Pit)), {t,
0, Infinity}]]
N[Integrate[
Im[(1 + It)^(1/(1 + It))]/Sinh[Pit], {t, 0, Infinity}] ==
2Integrate[
Im[E^(Pit + Log[1 + It]/(1 + It))]/(E^(PiI) + E^(2Pit)), {t,
0, Infinity}]]
Also, we can take the imaginary part of the outside in the following.
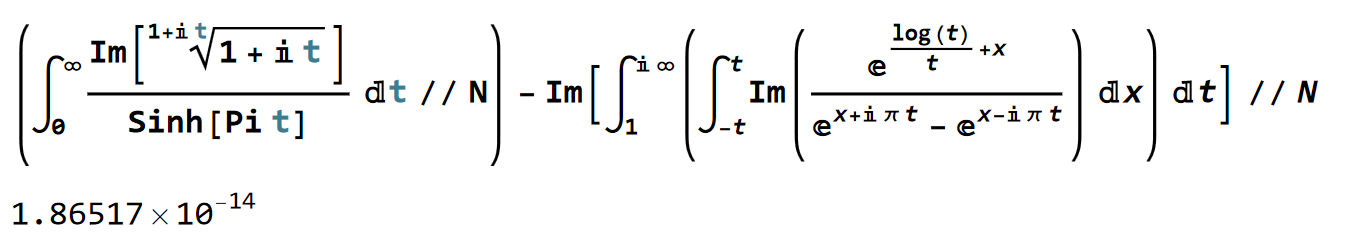
N[Integrate[
Im[(1 + I*t)^(1/(1 + I*t))]/Sinh[Pi*t], {t, 0, Infinity}]] -
N[Im[Integrate[
Integrate[
Im[E^(Log[t]/t + x)/(E^(x + I*Pi*t) - E^(x - I*Pi*t))], {x, -t,
t}], {t, 1, I*Infinity}]]]
Regressing to the flow of "MRB constant Absolute Convergence
an Analog to the Exponential Function
Leading to an Integral Representation,"
The connection between the MRB constant and the integral expression involving complex functions arises from advanced mathematical analysis and the exploration of series convergence properties through complex analysis techniques.
High level proof of
$$C_{MRB} = \int_{0}^{\infty} \frac{\Im (f(t))}{\sinh(\pi t)} dt $$
without the Abel-Plana theorem
by the Wolfram Notebook Assistant
Certainly! Here's a condensed version of your proof, maintaining all
the critical computations and steps:
Proving the Connection between the MRB Constant and its Integral Representation
This proof involves complex analysis, asymptotic analysis, and special
functions to establish the relationship between the MRB constant and
its integral form.
1. Series Representation
Define the MRB constant as an alternating series:
$$\text{MRB} =
\sum_{n=1}^{\infty} (-1)^n (n^{1/n} - 1)$$
2. Complex Function Representation
Consider the complex function:
$$(1 + it)^{1/(1 + it)}$$ This
function captures the essence of the series term
$$n^{1/n}$$ and can
be expanded to show its behavior in the complex plane.
3. Integral Representation
The integral:
$$\text{CMRB} = \int_0^\infty \text{Im}\left[(1 +
it)^{1/(1 + it)} \text{Csch}(\pi t)\right] \, dt$$ connects the series
with the integral using complex analysis techniques.
4. Asymptotic Analysis and Convergence
Analyze the asymptotic behavior of
$$(1 + it)^{1/(1 + it)}$$ and
$$\text{Csch}(\pi t)$$ to ensure the integral converges, examining
$$t
\to 0$$ and
$$t \to \infty$$.
5. Relate Series Terms to Integral Components
Expand the complex function
$$f(t) = (1 + it)^{1/(1 + it)}$$ as:
$$f(t) \approx 1 + a_1 t + a_2 t^2 + \cdots$$ Extract the imaginary
part:
$$\text{Im}[f(t)] \approx b_1 t + b_3 t^3 + \cdots$$ Relate
these terms to the MRB series, highlighting the alternating nature
with
$$(-1)^n n^{1/n}$$.
6. Use Analytic Continuation
If necessary, utilize analytic continuation to explore the series and
integral in a unified framework.
7. Convergence Analysis
At Infinity: Analyze
$$\text{Im}[f(t)] \text{Csch}(\pi t)$$ to confirm convergence with damping by
$$\text{Csch}(\pi t)$$.
Near Zero: Assess behavior around
$$t = 0$$ using the series expansion.
8. Numerical Verification
Perform numerical computations for both the MRB series and the
integral, ensuring they converge to the same value. Truncate and
compare finite sums to verify consistency.
**Here is a program I wrote that ensures they converge to the same value, as well as, perhaps asymptotically by the expression ![(2sin(1))/(tsinh([Pi] t))](https://community.wolfram.com//c/portal/getImageAttachment?filename=Screenshot2025-04-06011559.png&userId=366611) , where t is the precision. **
, where t is the precision. **
Conclusion
By expanding the complex function, analyzing convergence, and verifying numerically, we establish a robust connection between the MRB constant and its integral representation. This approach not only proves the equivalence but also deepens our understanding of the underlying mathematical structures.
This condensed proof outlines the critical steps and computations needed to establish the connection, focusing on the interplay between series terms and their integral counterparts.
While the proof requires a deep understanding of complex analysis and asymptotic methods, the crux lies in showing that the complex integral captures the oscillatory and convergence behavior of the MRB series through a carefully constructed analytic expression. This approach not only proves the connection but also enriches our understanding of the MRB constant's mathematical nature.
A lower-level proof follows from the proceeding sum-integral identity.
Yet another MRB constant integral
On Pi Day, 2021, 2:40 pm EST,
I added a new MRB constant integral. Surprisingly to me, this one is proven by the mere definition of the Residue Theorem: With additional thought, the previous sum-integral and this integral-sum can be seen as the same identity or relation by a factor of i, so this new proof solidifies our high-level one. The Wolfram Assistant proved it.



Proof:

The notebook assitant clarified:
The appearance of the cosine function in the series is due to how the
real part of the integral and the series terms are related, rather
than a direct transformation of Csc into Cos. The real part of the
expression and the periodicity of cosine (due to the integer poles
considered) naturally lead to the involvement of cosine in the final
expression.

Conclusion
This proof shows how the original integral can be transformed into an infinite series by leveraging complex analysis techniques, specifically contour integration and the residue theorem. Each step builds on the analytical properties of the function and the behavior of its poles in the complex plane.