So I am building an availability analysis model and was looking for help on how to code certain things. The typical approach to the problem uses LaPlace transforms and is relatively neat, but my professor wants me to see if it is possible to "do it the long way". My overall availability function is represented as
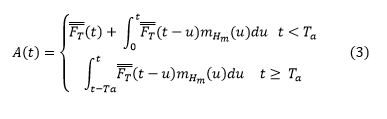
Where F(t) bar is the survival function of a truncated exponential, Ta is a constant and m(u) is the renewal density which is found by doing the following: First finding the overall distribution on the interval hm(t) which is not shown because it is long and tedious.Then a recursive function is used to find the power convolutions using for k = 0 to infinity:
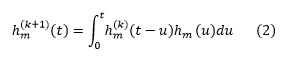
The k-fold (or n-fold) convolution is the sum of these iterations up to infinity. Luckily as k increases, the overall effect becomes negligible (so if k=15 for example, the overall summation would not actually change). So I have been working just the first few values of k. 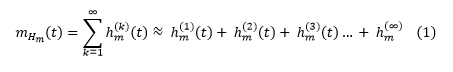
So a few questions... For the Availability function, how can I define this convolution/integral with those bounds? It is killing me... Is there a better way to do a k-fold convolution? To give some perspective on how long this code takes to run, I started taking convolutions for different values of k in (2) and the first one took 7 minutes to run... Also, when should I use full simplify vs simplify? I can post some code below to help. I have been working on this one problem for over a month, any help would be greatly appreciated.
gr[t_] = PDF[ExponentialDistribution[mur], t]
fot[t_] = PDF[TruncatedDistribution[{0, ta}, ExponentialDistribution[lam]], t]
hr = Convolve[fot[u], gr[u], u, t] // FullSimplify
hp = PDF[TransformedDistribution[u + ta, u \[Distributed] ExponentialDistribution[mup]], t]`
hm[t_] = Evaluate[CDF[ExponentialDistribution[lam], t] /. t -> ta]*hr + Evaluate[(1 - CDF[ExponentialDistribution[lam], t]) /. t -> ta]*hp // FullSimplify
hm2[t_] := Convolve[hm[u], hm[u], u, t] // Simplify
hm3[t_] := Convolve[hm2[u], hm[u], u, t] // Simplify
mh[t_] = hm[t] + hm2[t] // Simplify
My output for hm(t) is below, when I substitute numerical values for ta, lam, mup I don't get the nonsense parts of the piecewise so I am not too worried. 
Again, any help at all would be greatly appreciated.