Hi, I am trying to calculate mean curvature of a parametric surface(like sphere), and I wrote this code based on this discussion. Here is my code:
MeanCurvature[(f_)?VectorQ, {u_, v_}] :=
Simplify[(-2*D[f, {u}] . D[f, {v}]*
Det[{D[f, {u}, {v}], D[f, {u}], D[f, {v}]}] +
Abs[D[f, {v}] . D[f, {v}]]*
Det[{D[f, {u, 2}], D[f, {u}], D[f, {v}]}] +
Abs[D[f, {u}] . D[f, {u}]]*
Det[{D[f, {v, 2}], D[f, {u}], D[f, {v}]}])/
(2*
PowerExpand[
Simplify[
Abs[D[f, {u}] . D[f, {u}]]*
Abs[D[f, {v}] . D[f, {v}]] - (D[f, {u}] . D[f, {v}])^2]^(3/
2)])];
Options[gccolor] =
Select[Options[ParametricPlot3D],
FreeQ[#1, ColorFunctionScaling] & ];
Off[RuleDelayed::rhs];
signgccolor[f_, {u_, ura__}, {v_, vra__}, (opts___)?OptionQ] :=
Module[{cf, gc, rng},
cf = ColorFunction /. {opts} /. Options[gccolor];
If[cf === Automatic,
cf = Which[Positive[#1], RGBColor[#1/(#1 + 1), 0, 0],
Negative[#1], RGBColor[0, 0, -(#1/(1 - #1))], True,
RGBColor[1, 1, 1]] & ];
gc[u_, v_] = MeanCurvature[f, {u, v}];
ParametricPlot3D[f, {u, ura}, {v, vra},
ColorFunction -> Function[{x, y, z, u, v}, cf[gc[u, v]]],
ColorFunctionScaling -> False,
Evaluate[FilterRules[{opts}, Options[gccolor]]]]];
On[RuleDelayed::rhs];
rng = {NMinValue[{MeanCurvature[{Cos[u]*Cos[v], Sin[u]*Cos[v],
Sin[v]}, {u, v}], -(Pi/2) < u < Pi/2 && 0 < v < 2*Pi}, {u, v}],
NMaxValue[{MeanCurvature[{Cos[u]*Cos[v], Sin[u]*Cos[v],
Sin[v]}, {u, v}], -(Pi/2) < u < Pi/2 && 0 < v < 2*Pi}, {u, v}]}
range = {-1.0000000000000002, 1.0000000000000002} this is the first problem! mean curvature of a sphere is a constant positive number.
twist = signgccolor[{Cos[u]*Cos[v], Sin[u]*Cos[v],
Sin[v]}, {u, -(Pi/2), Pi/2}, {v, 0, 2*Pi},
ColorFunction -> (Glow[
Which[Positive[#1], Lighter[Red, Rescale[#1, {0, 1}, {1, 0}]],
Negative[#1], Lighter[Blue, Rescale[#1, {0, -1}, {1, 0}]],
True,
White]] & )]
Animate[With[{v = RotationTransform[\[Theta], {0, 0, 1}][{3, 0, 3}]},
Show[twist, ViewPoint -> v, SphericalRegion -> True,
Boxed -> False, Axes -> False]],
{\[Theta], 0, 2*Pi}, AnimationRate -> 0.1,
AnimationRunning -> True]
and the output looks like this: 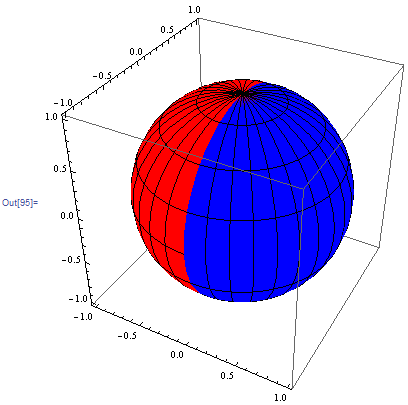
How can I fix this problem? I've checked the formula and I don't think that its wrong.