Message Boards Message Boards

1
|
5990 Views
|
10 Replies
|
5 Total Likes
View groups...
Share
Share this post:

NDSolve - Can anyone see what's wrong in my thinking?

David Keith
Posted 10 years ago

Here is a simple differential-algebraic equation. I think that since d[t] has a delta at t=10, s[t] should step up at that point. But it steps down.

eqs1 = {
   s'[t] == d[t] - s[t]/10,
   s[0] == 0,
   d[t] == DiracDelta[t - 10]
   };

ss1 = NDSolveValue[eqs1, s, {t, 0, 100}];

p1 = Plot[ss1[t], {t, 0, 100}, PlotRange -> All]

enter image description here

This did not seem right, but to check I made the sign in front of d[t] in the first equation negative:

(* note the - sign in front of d[t] *)

eqs2 = {
   s'[t] == -d[t] - s[t]/10,
   s[0] == 0,
   d[t] == DiracDelta[t - 10]
   };

ss2 = NDSolveValue[eqs2, s, {t, 0, 100}];

p2 = Plot[ss2[t], {t, 0, 100}, PlotRange -> All]

enter image description here

But it does not seem to matter!
POSTED BY: David Keith
10 Replies
Sort By:

Just to follow up: a bug has been filed on this.
POSTED BY: Daniel Lichtblau
David Keith
David Keith
Posted 10 years ago

Thank you.
POSTED BY: David Keith

The unexpected behaviour of the negative peak reported by David still occurs in Wolfram 14.1.
POSTED BY: Asmus Meyer-Plath
David Keith
David Keith
Posted 10 years ago

Thanks, Daniel. And that is interesting. Your code produces correct results when the delta function is included in the single equation system. Mine apparently gets the sign wrong when the delta function is split out into a second equation.

I do get your point about numerically handling the delta function. The routine must understand when it has integrated over it, and I would think that would be troublesome for convergence. And it would of course be possible to use a delta function where it escaped from under the integral, and became a monster.

I also see that WhenEvent provides a perfectly good way of handling this. The only purpose of the delta under the integral is to increment the solution at that point, which can easily be done with WhenEvent. (WhenEvent was a great addition.)

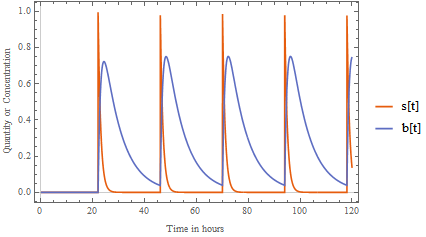
For anyone interested, I ran into this just playing around. Suppose one takes a dose of medication every day at 10PM (2200). The dose moves to the bloodstream with a time constant of 1 hour. In the bloodstream, the concentration decays with a time constant of 7 hours. What is the quantity in the stomach and the blood over time?

eqs = {
   (* stomach *)
   s'[t] == -s[t]/ts,
   (* bloodstream *)
   b'[t] == s[t]/ts - b[t]/tb,
   s[0] == 0,
   b[0] == 0,
   (* dose at 10PM *)
   WhenEvent[Mod[t - 22, 24] == 0, s[t] -> s[t] + d]
   };

{ss, bb} = 
  NDSolveValue[eqs /. {ts -> 1, tb -> 7, d -> 1}, {s, b}, {t, 0, 120}];

Plot[{ss[t], bb[t]}, {t, 0, 120}, PlotLegends -> {"s[t]", "b[t]"}, 
 FrameLabel -> {"Time in hours", "Quantity or Concentration"}, 
 PlotTheme -> "Scientific"]

enter image description here
POSTED BY: David Keith

I am not familiar with the code internals but I can easily imagine that a Dirac delta will pose difficulties for any numerical software. There are, however, numerous ways to handle discrete events in NDSolve. There is a very thorough discussion of this in the Documentation Center, under tutorial/NDSolveWhenEvents.

One thing that, err, bugs me though. Both of the variants below get the desired result.

eqs1 = {s'[t] == DiracDelta[t - 10] - s[t]/10, s[0] == 0};
ss1 = NDSolveValue[eqs1, s, {t, 0, 100}];
p1 = Plot[ss1[t], {t, 0, 100}, PlotRange -> All]

eqs1 = {s'[t] == d[t] - s[t]/10, s[0] == 0} /.  d[t] -> DiracDelta[t - 10];
ss1 = NDSolveValue[eqs1, s, {t, 0, 100}];
p1 = Plot[ss1[t], {t, 0, 100}, PlotRange -> All]
POSTED BY: Daniel Lichtblau
David Keith
David Keith
Posted 10 years ago

Thanks, David. Interesting. And thanks for reporting it. Regarding my Yikes above, I found one of those on my kitchen wall an hour ago. So it may have escaped.
POSTED BY: David Keith

Note that DSolve does give the correct solution:

In[21]:= eqs = {s'[t] == d[t] - s[t]/10, s[0] == 0, 
   d[t] == DiracDelta[t - 10]};

DSolveValue[eqs, s[t], t]

Out[22]= E^(1 - t/10) HeavisideTheta[-10 + t]

and 

Plot[E^(1 - t/10) HeavisideTheta[-10 + t], {t, 0, 100}, PlotRange -> All]

gives

enter image description here

I have reported the bug....
POSTED BY: David Reiss

Yes...

Style[\[FreakedSmiley], 100]

enter image description here
POSTED BY: David Reiss
David Keith
David Keith
Posted 10 years ago

Yikes! enter image description here
POSTED BY: David Keith

Strangely the following (which crudely mocks up the delta function with UnitStep functions) works as you expect it to (and as you expect your original system to work):

eqs1 = {s'[t] == d[t] - s[t]/10, s[0] == 0,
   d[t] == UnitStep[t - 10] - UnitStep[t - 11]};

ss1 = NDSolveValue[eqs1, s, {t, 0, 100}];

p1 = Plot[ss1[t], {t, 0, 100}, PlotRange -> All]

enter image description here

It looks like you found a bug...
POSTED BY: David Reiss
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract