I want to find the roots of an equation using FindRoot as a function of a real parameter K and then plot the real and imaginary solutions vs. the parameter K. The function I'm trying to find the roots is:
f[\[CapitalOmega]_,K_]:=1.`\[VeryThinSpace]+(0.00021600988594924262` K^10+(3.81005811091083`*^-6-5.617765774643865`*^-9 I) K^2 \[CapitalOmega]^8-(1.938898556339015`*^-8-4.736384338194926`*^-11 I) \[CapitalOmega]^10+K^4 \[CapitalOmega]^6 ((-0.00024705957314623457`+1.7313407860214411`*^-7 I)+1.3234889800848443`*^-23 \[CapitalOmega]^2)+K^6 \[CapitalOmega]^4 ((0.005208736011404687`\[VeryThinSpace]+8.502422744684232`*^-8 I)+4.235164736271502`*^-22 \[CapitalOmega]^2)+K^8 \[CapitalOmega]^2 ((0.0021316316776359315`\[VeryThinSpace]+1.0578397620930897`*^-8 I)+6.776263578034403`*^-21 \[CapitalOmega]^2))/(2.138711742071709`*^-6 K^12+0.000021082195553663905` K^10 \[CapitalOmega]^2+0.000051246570978881814` K^8 \[CapitalOmega]^4-3.481280809505708`*^-6 K^6 \[CapitalOmega]^6+8.665879028798112`*^-8 K^4 \[CapitalOmega]^8-9.45611694948034`*^-10 K^2 \[CapitalOmega]^10+3.831913991301718`*^-12 \[CapitalOmega]^12)
The real solutions Wr :
Subscript[W, r][K_,\[Mu]_]:=Re[\[CapitalOmega]/.FindRoot[1.+(0.00021600988594924262 K^10+(3.81005811091083*^-6-5.617765774643865*^-9 I) K^2 \[CapitalOmega]^8-(1.938898556339015*^-8-4.736384338194926*^-11 I) \[CapitalOmega]^10+K^4 \[CapitalOmega]^6 ((-0.00024705957314623457+1.7313407860214411*^-7 I)+1.3234889800848443*^-23 \[CapitalOmega]^2)+K^6 \[CapitalOmega]^4 ((0.005208736011404687+8.502422744684232*^-8 I)+4.235164736271502*^-22 \[CapitalOmega]^2)+K^8 \[CapitalOmega]^2 ((0.0021316316776359315+1.0578397620930897*^-8 I)+6.776263578034403*^-21 \[CapitalOmega]^2))/(2.138711742071709*^-6 K^12+0.000021082195553663905 K^10 \[CapitalOmega]^2+0.000051246570978881814 K^8 \[CapitalOmega]^4-3.481280809505708*^-6 K^6 \[CapitalOmega]^6+8.665879028798112*^-8 K^4 \[CapitalOmega]^8-9.45611694948034*^-10 K^2 \[CapitalOmega]^10+3.831913991301718*^-12 \[CapitalOmega]^12),{\[CapitalOmega],K/Sqrt[\[Mu] (1+K^2)]}]];
And the imaginary solutions Wi :
Subscript[W, i][K_,\[Mu]_]:=Im[\[CapitalOmega]/.FindRoot[1.`\[VeryThinSpace]+(0.00021600988594924262` K^10+(3.81005811091083`*^-6-5.617765774643865`*^-9 I) K^2 \[CapitalOmega]^8-(1.938898556339015`*^-8-4.736384338194926`*^-11 I) \[CapitalOmega]^10+K^4 \[CapitalOmega]^6 ((-0.00024705957314623457`+1.7313407860214411`*^-7 I)+1.3234889800848443`*^-23 \[CapitalOmega]^2)+K^6 \[CapitalOmega]^4 ((0.005208736011404687`\[VeryThinSpace]+8.502422744684232`*^-8 I)+4.235164736271502`*^-22 \[CapitalOmega]^2)+K^8 \[CapitalOmega]^2 ((0.0021316316776359315`\[VeryThinSpace]+1.0578397620930897`*^-8 I)+6.776263578034403`*^-21 \[CapitalOmega]^2))/(2.138711742071709`*^-6 K^12+0.000021082195553663905` K^10 \[CapitalOmega]^2+0.000051246570978881814` K^8 \[CapitalOmega]^4-3.481280809505708`*^-6 K^6 \[CapitalOmega]^6+8.665879028798112`*^-8 K^4 \[CapitalOmega]^8-9.45611694948034`*^-10 K^2 \[CapitalOmega]^10+3.831913991301718`*^-12 \[CapitalOmega]^12),{\[CapitalOmega],K/Sqrt[\[Mu](1+K^2)]}]];
When I plotted the real part Wr I got the following numerical roundoff error :
Block[{\[Mu] = 100}, Plot[{Subscript[W, r][K, \[Mu]]}, {K, 0, 5}, Frame -> True, PlotRange -> {0, 0.2}, PlotRangePadding -> 0, WorkingPrecision -> 100]]
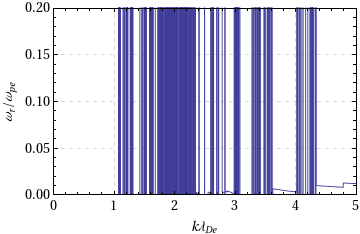
And When I plotted the imaginary part Wi I got also the numerical roundoff error :
Block[{\[Mu] = 100},
Plot[{-Subscript[W, i][K, \[Mu]] }, {K, 0, 5}, Frame -> True,
PlotRange -> {0, 0.02}, PlotRangePadding -> 0,
WorkingPrecision -> 100]]
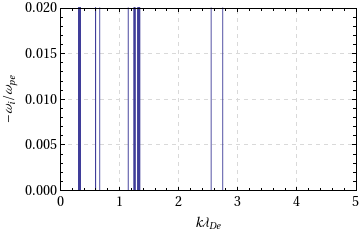
Please, Can you give me now some hint here? I confess that I' m not very savvy with Mathematica and don' t really know which methods are implemented.
 Attachments:
Attachments: