Here is my latest attempt to find a super-fast method of computing the MRB constat as of 11/18/2014. (I still have a ways to go.) See http://community.wolfram.com/groups/-/m/t/366628?p_p_auth=90Hj0Sid for my attempts at computing it. The notebook is attached so you can copy and edit it.

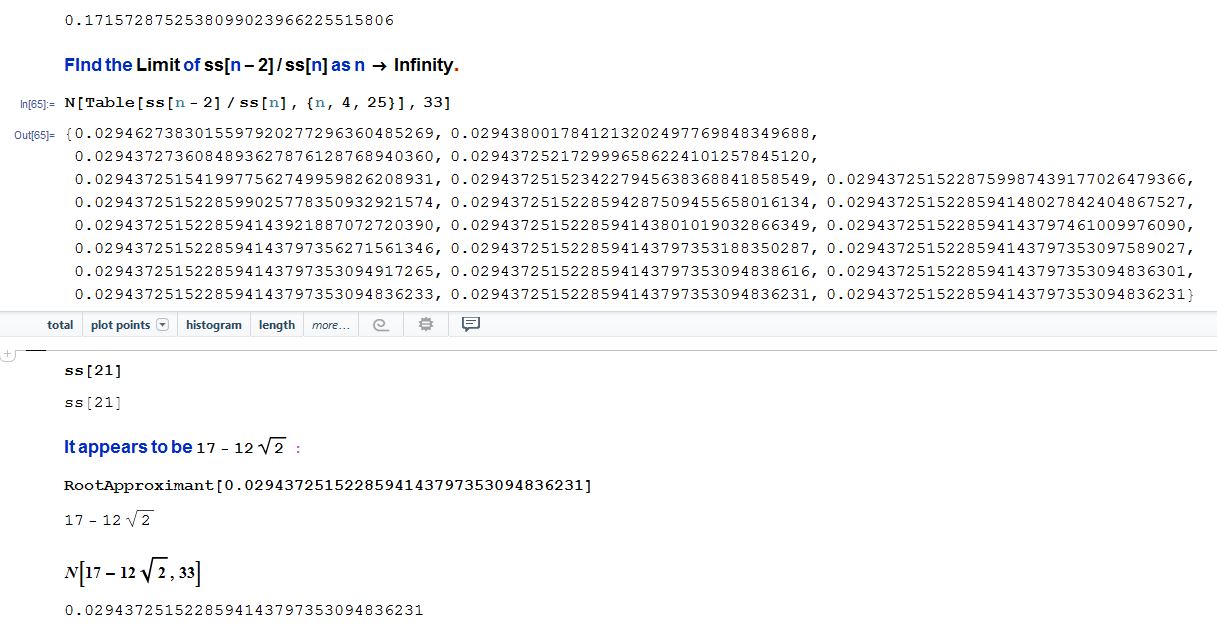

Reconstruct and greatly expand the above RootApproximant's (here f) and find they are approximated well by certain
((1+Sqrt[2])^n+(1-Sqrt[2])^n)/2.
Clear[key, f]
Block[{$MaxExtraPrecision = 1000}, For[x = 1, x <= 48,
key[x] = Table[Convergents[Sqrt[2], 100][[2 n]], {n, 50}][[-x]];
f[x] = Numerator[key[x]] - Denominator[key[x]] Sqrt[2];
Print[N[((1 + Sqrt[2])^n + (1 - Sqrt[2])^n)/2 /. n -> 100 + 2 (x - 1),
120 + x] - N[f[x], 120 + x]*ChebyshevT[100, 3]];
x++]]
2.6387695903457195648070395905136485002528815*10^-39
4.527412857479332018505153596026307976091567*10^-40
7.767812414187964629605256710213628540205842*10^-41
1.332745910334467592580004301018691480319384*10^-41
2.28663047818840925874769095898520341710461*10^-42
3.9232376578577962668610274372430569943380*10^-43
6.7312116526268501368925503360630779498198*10^-44
1.1548933371831381527450276439478977555385*10^-44
1.981483704719787795776155276243085834114*10^-45
3.39968856487345247206655217979537449296*10^-46
5.83294342042836874637760316341388616634*10^-47
1.00077487383568775760009718252957206843*10^-47
1.7170582258575779922297993176354624423*10^-48
2.946006167885903773778240805170539698*10^-49
5.054547487396427203714516546686137636*10^-50
8.67223245519525484504691228411428839*10^-51
1.48791985720725703313630823782435395*10^-51
2.5528668804828735377093714283183531*10^-52
4.380027108246708948931461916665789*10^-53
7.514938446515183164950572168112005*10^-54
1.289359596624009500388813842014146*10^-54
2.21219133228873837382310883972869*10^-55
3.7955202749233523905051461823070*10^-56
6.5120832665273060479978869655528*10^-57
1.1172968499303123829358599702467*10^-57
1.916978330545682496172728559273*10^-58
3.28901483970971147677771653172*10^-59
5.64305732801443898939013597563*10^-60
9.6819557098951916856365053661*10^-61
1.6611609792267602199176724406*10^-61
2.850101654653696338695292773*10^-62
4.89000135654575832995032232*10^-63
8.38991592737586592749006203*10^-64
1.43948199879761226543714897*10^-64
2.4697606540980766513283182*10^-65
4.237439366123372535984192*10^-66
7.270296557594687026219692*10^-67
1.247385684334396797476231*10^-67
2.14017548411693758637696*10^-68
3.6719606135765754349947*10^-69
6.3000884029007674619849*10^-70
1.0809242816388504219628*10^-70
1.854572869323350697919*10^-71
3.18194399551599967885*10^-72
5.45935279862491093918*10^-73
9.3667683658946884656*10^-74
1.6070822091190214020*10^-74
2.757248888194399464*10^-75
 Attachments:
Attachments: