This example goes wrong. Thank you for pointing that out. That happened because SortBy ignores the numerical value

In[27]:= qS =  SortBy[Partition[{{4, 5}, {0, 0}, {15/2, 5/2}}, 2, 1, 1], Norm[Subtract @@ #] &]
Out[27]= {{{0, 0}, {15/2, 5/2}}, {{15/2, 5/2}, {4, 5}}, {{4, 5}, {0, 0}}}

In[28]:= qS = EuclideanDistance @@@ SortBy[Partition[{{4, 5}, {0, 0}, {15/2, 5/2}}, 2, 1, 1], Norm[Subtract @@ #] &]
Out[28]= {5 Sqrt[5/2], Sqrt[37/2], Sqrt[41]}

In[29]:= N[qS]
Out[29]= {7.90569, 4.30116, 6.40312}

In[30]:= LeafCount /@ qS
Out[30]= {9, 7, 5}

Sort on the set {5 Sqrt[5/2], Sqrt[37/2], Sqrt[41]} respects neither the numerical value nor the LeafCount.

 In[31]:= Sort[{5 Sqrt[5/2], Sqrt[37/2], Sqrt[41]}]
 Out[31]= {5 Sqrt[5/2], Sqrt[37/2], Sqrt[41]}

 In[32]:= OrderedQ[Sort[{5 Sqrt[5/2], Sqrt[37/2], Sqrt[41]}]]
 Out[32]= True

 In[33]:= OrderedQ [LeafCount /@ {5 Sqrt[5/2], Sqrt[37/2], Sqrt[41]}]
 Out[33]= False

this is a bit over-canonical but it is as it is. Well. Let's change the norm again to fix that

Clear[ledesmaQuarter, triangleQ, q, q4, orie]
orie[p1_List, p2_List, p3_List] := If[Det[{p1 - p3, p2 - p3}] > 0, {p1, p2}, {p2, p1}]
q4[l_List] := 
 Block[{qS = Sort[Partition[l, 2, 1, 1], (EuclideanDistance @@ #1) < (EuclideanDistance @@ #2) &],
   p01, p02, p03, p11, p12, p13},
  (* triangle has points p01,p02,p03 *)
  (* orient the triangle *)
  (* the biggest angle (vertex p01) is opposite to the longest edge, 
  find it's midpoint: p11 *)
  (* get the midpoint of the legs of the biggest angle: p12, p13 *)
  {p02, p03} = qS[[-1]]; p01 = Complement[l, qS[[-1]]][[1]];
  {p02, p03} = orie[p02, p03, p01];
  {p13, p12, p11} = (Plus[#[[1]], #[[2]]]/2)& /@ qS;
  {p12, p13} = orie[p12, p13, p11];
  {{p01, p13, p11}, {p13, p02, p11}, {p11, p03, p12}, {p12, p01, p11}}
  ]
q[l_List] := Flatten[q4 /@ l, 1]
triangleQ[l_List] := If[Length[l] != 3, False,
  If[Chop[Area[Triangle[l]]] == 0, False,
   True]
  ]
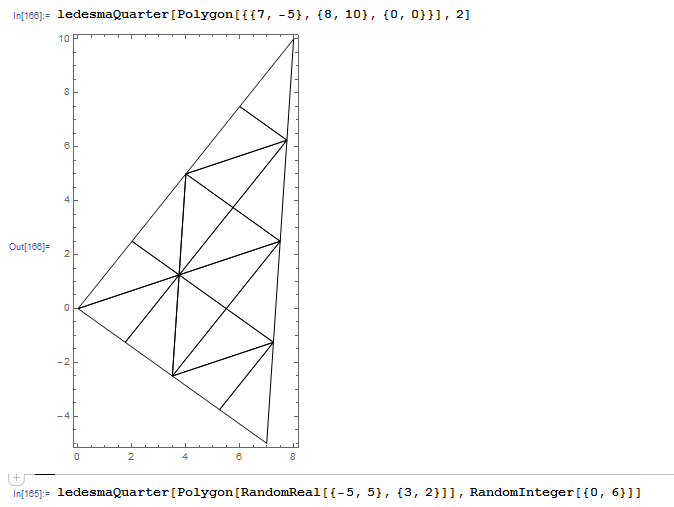
ledesmaQuarter[l_Polygon (* a triangle *), 
  n_Integer?NonNegative(* number of sections *)] := 
 Module[{l0 = Sequence @@ l},
  If[! triangleQ[l0],
   Print["Polygon ", l, " is not a triangle."];
   Return[$Failed]
   ];
  Graphics[Line[Join[#, {First[#]}]& /@ Nest[q, {l0}, n]], Frame -> True]
  ]

and look again at the test triangle

With respect to the interesting triangulation video made by your friend, have you seen Vitaliy's post Your own personal digital Rosetta Comet, especially the MeshRegion? I presume it's possible to redo your friend's program in Mathematica, but I'm not going to proof that.

Udo thank you very much for your help, I have no words to thank you've solved my problem, i will be testing your code with several triangles, thank you once again, you have shown me that I have a lot to learn from Mathematica, and for advanced users such as you.

I've still an orientation error in it

It was not an orientation error, but an abuse of Norm for the data structure chosen; now it runs

Clear[triangleQ, q4, q, ledesmaQuarter]
triangleQ[l_List] := If[Length[l] != 3, False,
  If[Chop[Area[Triangle[l]]] == 0, False,
   True]
  ]
q4[l_List] := 
 Block[{qS = SortBy[Partition[l, 2, 1, 1], Norm[Subtract @@ #] &],
   p01, p02, p03, p11, p12, p13},
  (* triangle has points p01,p02,p03 *)
  (* orient the triangle *)
  (* the biggest angle (vertex p01) is opposite to the longest edge, 
  find it's midpoint: p11 *)
  (* get the midpoint of the legs of the biggest angle: p12, p13 *)
  {p02, p03} = qS[[-1, 1 ;; 2]]; p01 = Complement[l, qS[[-1]]][[1]];
  If[Last[Cross[Join[p02 - p01, {0}], Join[p03 - p01, {0}]]] < 0,
   {p02, p03} = {p03, p02}
   ];
  {p13, p12, p11} = (Plus[#[[1]], #[[2]]]/2) & /@ qS;
  If[Last[Cross[Join[p12 - p11, {0}], Join[p13 - p11, {0}]]] < 0,
   {p12, p13} = {p13, p12}
   ];
  {{p01, p13, p11}, {p13, p02, p11}, {p11, p03, p12}, {p12, p01, p11}}
  ]
q[l_List] := Flatten[q4 /@ l, 1]
ledesmaQuarter[l_Polygon (* a triangle *), 
  n_Integer?Positive (* number of sections *)] := 
 Module[{l0 = Sequence @@ l},
  If[! triangleQ[l0],
   Print["Polygon ", l, " is not a triangle."];
   Return[$Failed]
   ];
  Graphics[Line[Join[#, {First[#]}] & /@ Nest[q, {l0}, n]], 
   Frame -> True]
  ]

Thank you for sharing the error that had my picture,The problem originated in my routine that programming in mathematica here the share

ang[vert_] :=  
 Module[{m1, m2, m3, \[Theta]1, \[Theta]2, \[Theta]3, masi, pmo, 
   mitlad1, mitlad2},
  m1 = (vert[[2, 2]] - vert[[1, 2]])/(vert[[2, 1]] - vert[[1, 1]]);
  m2 = (vert[[3, 2]] - vert[[1, 2]])/(vert[[3, 1]] - vert[[1, 1]]);
  m3 = (vert[[3, 2]] - vert[[2, 2]])/(vert[[3, 1]] - vert[[2, 1]]);
  \[Theta]1 = ArcTan[(m2 - m1)/(1 + m2*m1)];
  \[Theta]3 = ArcTan[(m3 - m2)/(1 + m2*m3)];
  \[Theta]2 = ArcTan[(m1 - m3)/(1 + m3*m1)];
  masi = Flatten[
     Position[{\[Theta]1, \[Theta]2, \[Theta]3}, 
      Max[{\[Theta]3, \[Theta]2, \[Theta]1}]]][[1]];
  Which[masi == 3, 
   pmo = {(vert[[1, 1]] + vert[[2, 1]])/2, (
     vert[[1, 2]] + vert[[2, 2]])/2};
   mitlad1 = {(vert[[1, 1]] + vert[[3, 1]])/2, (
     vert[[1, 2]] + vert[[3, 2]])/2};
   mitlad2 = {(vert[[2, 1]] + vert[[3, 1]])/2, (
     vert[[2, 2]] + vert[[3, 2]])/2};
   {Line[{vert[[masi]], pmo}], Line[{mitlad1, pmo}], 
    Line[{mitlad2, pmo}]}
   ,
   masi == 2, 
   pmo = {(vert[[1, 1]] + vert[[3, 1]])/2, (
     vert[[1, 2]] + vert[[3, 2]])/2};
   mitlad1 = {(vert[[1, 1]] + vert[[2, 1]])/2, (
     vert[[1, 2]] + vert[[2, 2]])/2};
   mitlad2 = {(vert[[2, 1]] + vert[[3, 1]])/2, (
     vert[[2, 2]] + vert[[3, 2]])/2};
   {Line[{vert[[masi]], pmo}], Line[{mitlad1, pmo}], 
    Line[{mitlad2, pmo}]}
   ,
   masi == 1, 
   pmo = {(vert[[2, 1]] + vert[[3, 1]])/2, (
     vert[[2, 2]] + vert[[3, 2]])/2};
   mitlad1 = {(vert[[1, 1]] + vert[[2, 1]])/2, (
     vert[[1, 2]] + vert[[2, 2]])/2};
   mitlad2 = {(vert[[1, 1]] + vert[[3, 1]])/2, (
     vert[[1, 2]] + vert[[3, 2]])/2};
   {Line[{vert[[masi]], pmo}], Line[{mitlad1, pmo}], 
    Line[{mitlad2, pmo}]}
   ]
  ]

Where vert are the vertices of the triangle, and m1, m2, m3 are the slopes between points, theta1, theta2,theta3 are the internal angles of the triangle. As well when calculating

ang[{{0, 0}, {7/2, -(5/2)}, {15/2, 5/2}}]

I got that error,I hope someone can help me to correct this error for future things