Hi guys, I have been working on a project where I have to model the orbital velocity of a potential spacecraft and as I'm not too familiar with Mathematica it has been quite difficult. My question is if anyone could point out to me the error in my code or perhaps a way in which I could get the result to plot.
Here are the 4 differential equations that I need to solve for numerically using "NDSolve":
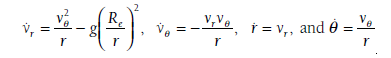
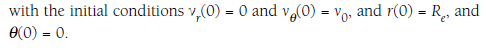
Where Re is equivalent to the radius of the earth 6400000m
g is equivalent to acceleration of gravity 9.8m/s
V_0 is also equal to a velocity of 7919.6m/s
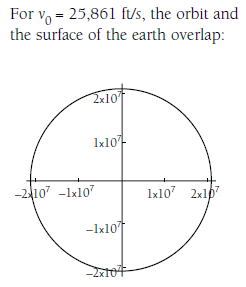
Over a period of 5077.6 seconds plot I'm looking to create should be similar to the plot shown below. Note: the plot shown below is in imperial but it represents the radius of the earth. The final plot from Mathematica would be somwhere in the 6*10^6 range.
Here is the code that I put into Mathematica and can't seem to get a result from Note: Vr=v, Vtheta = x, theta =y & r=z
solution = NDSolve[{
v'[t] == (((x[t])^2)/z[t]) - 9.8*((6400000/z[t])^2),
x'[t] == (-v[t]*x[t])/(z[t]),
z'[t] == v[t],
y' [t] == x[t]/z[t],
v[0] == 0,
x[0] == 7919.58,
z[0] == 6400000,
y[0] == 0 },
{v, x, z, y},
{t, 0, 5077.6}]
ParametricPlot[Evaluate[{z[t], y[t]} /. s], {t, 0, 5077.6}]
any ideas?