A vector geometry approach may be helpful.
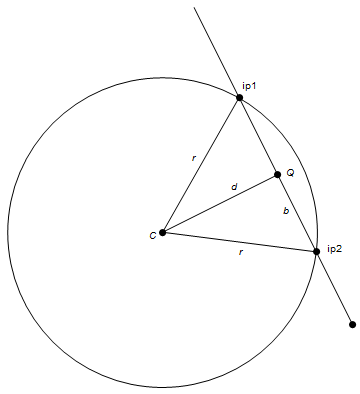
Let C be the circle center, r its radius.
Let P be a point on the line v, a unit vector in the direction of the line.
First, project C onto the line giving point Q
l = (C - P).v, Q = P + l v**.
Then compute the distance of C from the line
d = ||(C - Q)||
If this distance d = r, then Q is the tangent point.
If this distance d > r, then there are no real intersection points.
Else, the distance of the intersection points from Q are found using Pythagoras.
b = sqrt(r^2 - d^2)
then the two intersection points are given by:
ip1 = Q + b v, ip2 = Q - b v.