Splendid Can I have your adress mail

Bonnes et joyeuses fetes

André Dauphiné

Hi Andre,

it is not OK!

The solution in my response was just given in terms of your question. But a general remark must be made (as I found during a sleepless night): A Voronoi diagram basically deals with distances. Angular coordinates are therefore not appropriate here. If one wants to do it right, one has to perform a transformation into grid coordinates first. I tried, and my little code now looks like this:

ClearAll["Global`*"]

(* just 50 french cities are taken into account: *)
coord = Take[
   Table[CityData[c, "Coordinates"], {c, CityData[{All, "France"}]}], 
   50];

(* transformation from angular coordinates to grid-coordinates: *)
coordxy = 
  GeoGridPosition[
      GeoPosition[#, "WGS84"], {"UTMZone31", 
       "CentralScaleFactor" -> 0.9996, "GridOrigin" -> {500000, 0}}][[
     1]] & /@ coord;

(* now the voronoi tessellation is made: *)
border = ConvexHullMesh[coordxy];
voron = VoronoiMesh[coordxy];
chm = ConvexHullMesh @@@ MeshPrimitives[voron, 2];
ri = RegionIntersection[border, #] & /@ chm;
grLines = MeshPrimitives[#, 1] & /@ ri;

(* procedure for transformation graphics lines to GeoPath: *)
makeGeoPath[lineList_] := Module[{pts, geoPts},
  pts = lineList[[;; , 1, 1]];
  geoPts = 
   GeoPosition[GeoGridPosition[#, "UTMZone31"]] & /@ 
    Append[pts, pts[[1]]];
  GeoPath[geoPts]
  ]

(* show the result: *)
GeoGraphics[{Blue, makeGeoPath /@ grLines, Red,
   GeoMarker[GeoPosition /@ coord, \[FilledCircle]]}, 
 ImageSize -> Full]

The output then is:

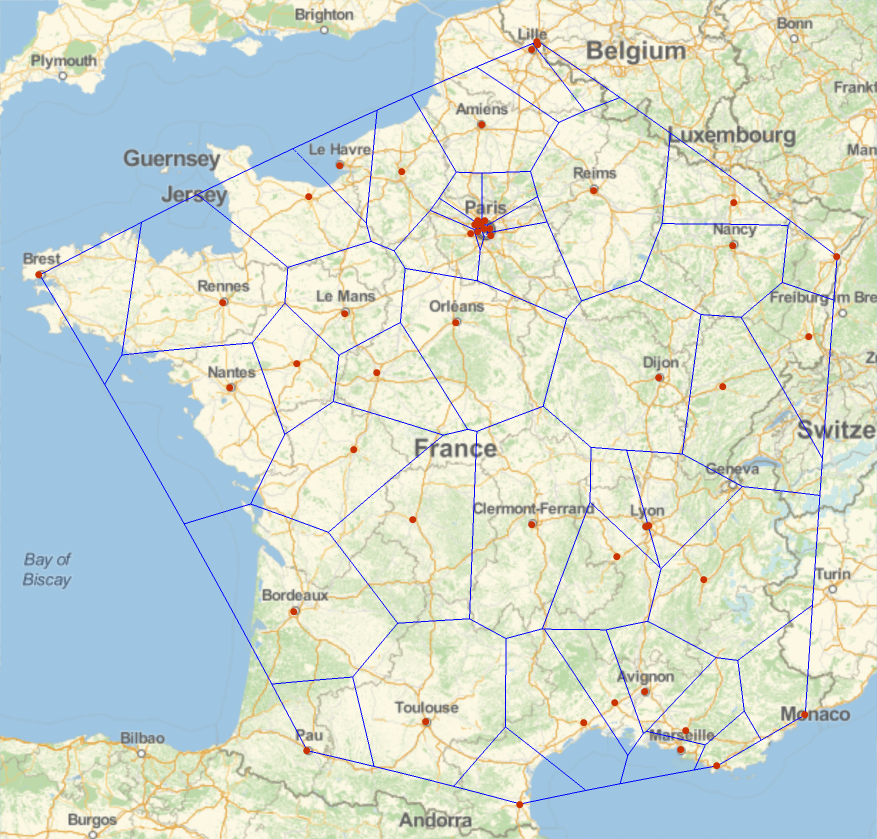
With using simply the angular coordinates, the result is just wrong:

Cheers Henrik

Unfortunately I do not have much experience in working with regions. But I find your question so interesting that I am trying now a "solution":

ClearAll["Global`*"]

pays = "France";
ny = ToExpression@
   DialogInput[
    DynamicModule[{name = ""}, 
     Column[{"How much cities?", InputField[Dynamic[name], String], 
       ChoiceButtons[{DialogReturn[name], DialogReturn[]}]}]]];
coord = Take[
   Table[Reverse[CityData[c, "Coordinates"]], {c, 
     CityData[{All, pays}]}], ny];
border = ConvexHullMesh[coord];   (* !!! *)
voron = VoronoiMesh[coord];
chm = ConvexHullMesh @@@ MeshPrimitives[voron, 2];

(* here is my idea: the individual intersection of the complete
region with every Voronoi tile: *)
ri = RegionIntersection[border, #] & /@ chm;
grLines = MeshPrimitives[#, 1] & /@ ri;
gr = Graphics[grLines]
DiscretizeGraphics[gr]

While this is quite a crude approach, I am sure there are much more elegant solutions. Maybe someone is going to give a hint.

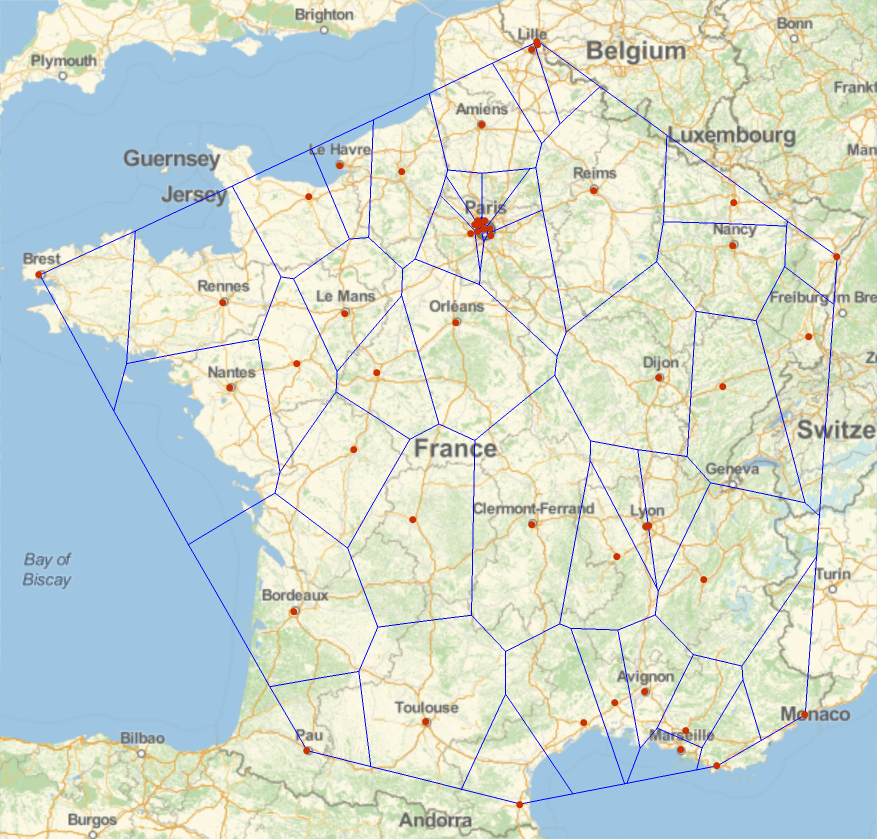
Cheers Henrik