A few methods of accelerating the convergence of alternating series is found here, written by Henri Cohen, Fernando Rodriguez Villegas, and Don Zagier, called Convergence Acceleration of Alternating Series . Here is a quote from it:.

Above where Cohen said,

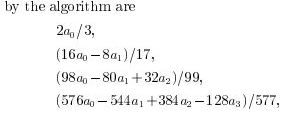
The denominators are Cos[x ArcCos[3]] and

the coefficients of the numerators are furthered below.

2
16, 8
98, 80, 32
576, 544, 384, 128
3362, 3312, 2912, 1792, 512
19600, 19528, 18688, 15104, 8192, 2048
114242, 114144, 112576, 103168, 76288, 36864, 8192
665856, 665728, 663040, 641536, 557056, 376832, 163840, 32768
3880898, 3880736, 3876416, 3832064, 3603968, 2945024, 1826816, 720896, 131072 

The first coefficient in each row is Cos[x ArcCos[3]]-1. Attached is some scratch work on finding a pattern for the second and third coefficients.

Does any body want to work on it?

Here is a sample of the file where I make use of the pattern "(2n^2 + 8n):"

In[172]:= nine = {3880898, 3880736, 3876416, 3832064, 3603968, 
  2945024, 1826816, 720896, 131072}

Out[172]= {3880898, 3880736, 3876416, 3832064, 3603968, 2945024, \
1826816, 720896, 131072}

In[173]:= Table[nine[[a]] - nine[[a + 1]], {a, 1, 8}]/9

Out[173]= {18, 480, 4928, 25344, 73216, 372736/3, 122880, 65536}



In[174]:= {480/18*3 - 10*8, 4928/480*15 - (2*7^2 + 8*7)}

Out[174]= {0, 0}






In[175]:= eight = {665856, 665728, 663040, 641536, 557056, 376832, 
  163840, 32768}

Out[175]= {665856, 665728, 663040, 641536, 557056, 376832, 163840, \
32768}

In[176]:= Table[eight[[a]] - eight[[a + 1]], {a, 1, 7}]/8

Out[176]= {16, 336, 2688, 10560, 22528, 26624, 16384}

In[177]:= {336/16*3 - 9*7, 2688/336*15 - (2*6^2 + 8*6)}

Out[177]= {0, 0}






In[178]:= seven = {114242, 114144, 112576, 103168, 76288, 36864, 8192}

Out[178]= {114242, 114144, 112576, 103168, 76288, 36864, 8192}

In[179]:= Table[seven[[a]] - seven[[a + 1]], {a, 1, 6}]/7

Out[179]= {14, 224, 1344, 3840, 5632, 4096}

In[180]:= {224/14*3 - 8*6, 1344/224*15 - (2*5^2 + 8*5)}

Out[180]= {0, 0}






In[181]:= six = {19600, 19528, 18688, 15104, 8192, 2048}

Out[181]= {19600, 19528, 18688, 15104, 8192, 2048}

In[182]:= Table[six[[a]] - six[[a + 1]], {a, 1, 5}]/6

Out[182]= {12, 140, 1792/3, 1152, 1024}

In[183]:= {140/12*3 - 7*5, (1792/3)/140*15 - (2*4^2 + 8*4)}

Out[183]= {0, 0}






In[184]:= five = {3362, 3312, 2912, 1792, 512}

Out[184]= {3362, 3312, 2912, 1792, 512}

In[185]:= Table[five[[a]] - five[[a + 1]], {a, 1, 4}]/5

Out[185]= {10, 80, 224, 256}

|

In[186]:= {80/10*3 - 6*4, 224/80*15 - (2*3^2 + 8*3)}

Out[186]= {0, 0}






In[187]:= four = {576, 544, 384, 128}

Out[187]= {576, 544, 384, 128}

In[188]:= Table[four[[a]] - four[[a + 1]], {a, 1, 3}]/4

Out[188]= {8, 40, 64}

In[189]:= {40/8*3 - 5*3, 64/40*15 - (2*2^2 + 8*2)}

Out[189]= {0, 0}






In[190]:= three = {98, 80, 32}

Out[190]= {98, 80, 32}

In[191]:= Table[three[[a]] - three[[a + 1]], {a, 1, 2}]/3

Out[191]= {6, 16}

(*{16/6*3-4*2,???????*)






In[192]:= two = {16, 8}

Out[192]= {16, 8}

In[193]:= Table[two[[a]] - two[[a + 1]], {a, 1, 1}]/2

Out[193]= {4}

Attachments: