Origami: Mathematica and Wolfram|Alpha Logos

I made these models as a gift for my geeky husband. Turns out these are great home decoration and cat toys! If you are interested in geeky home decoration or killing some time in a geeky way, try make your own origami logos follow the instruction below.
What's in the logo?
This blog post from WolframAlpha blog explained what the logos are in geometry. The origami models are made using unit origami method, that is making simple units and assemble them together to form a certain shape. Understanding the constituents of the logos might make the assembling easier.
Spikey
Mathematica logo v1 (Spikey) "consisted of the spiked solid obtained from an icosahedron (the regular 20-faced solid that is one of the five Platonic solids) with regular tetrahedra (triangular pyramids) affixed to its faces." Spikey has 60 equilateral triangular faces. Our basic unit contains two equilateral triangles, which means we need to make 30 units.
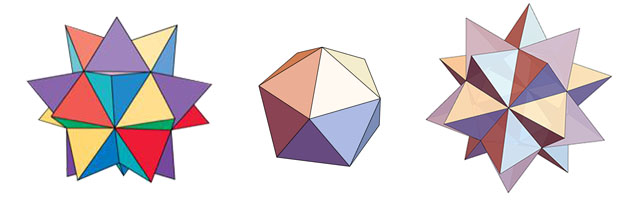
Wolfram|Alpha
The logo is a rhombic hexecontahedron (rhombic refers to the fact that the faces of the solid consist of rhombi, while hexecontahedron is a word derived from the Greek, which simply means 60-faced solid). The shape of the faces is called golden rhombus, which is very hard to construct in origami. Luckily this rhombus has an approximately 60 degree angle. I decided to use the same unit as Spikey. It needs 60 units to construct the Wolfram|Alpha logo.
You will need
- Origami paper: 30 pieces for Spikey and 60 pieces for Wolfram Alpha. If you use 7.5cm paper for Spikey or 5cm paper for Wolfram Alpha, your final work will be around 9cm in diameter.
- Knife: To cut paper in certain size.
- Glue: In fact you dont need anything like glue at all to finish the work. Just in case you want your model more stable and longer-lasting.
Tips
- Don't use thick paper for the work, as the folding gets very complicated in the end.
- If you decided not to use any glue, don't use slippery paper. It will drive you crazy!
- The folding gets easier when you use larger paper, but the assembling will be looser and harder to make last.
- Using professional origami paper will save you a lot of cutting effort.
Basic Unit Folding Instruction
Step 0
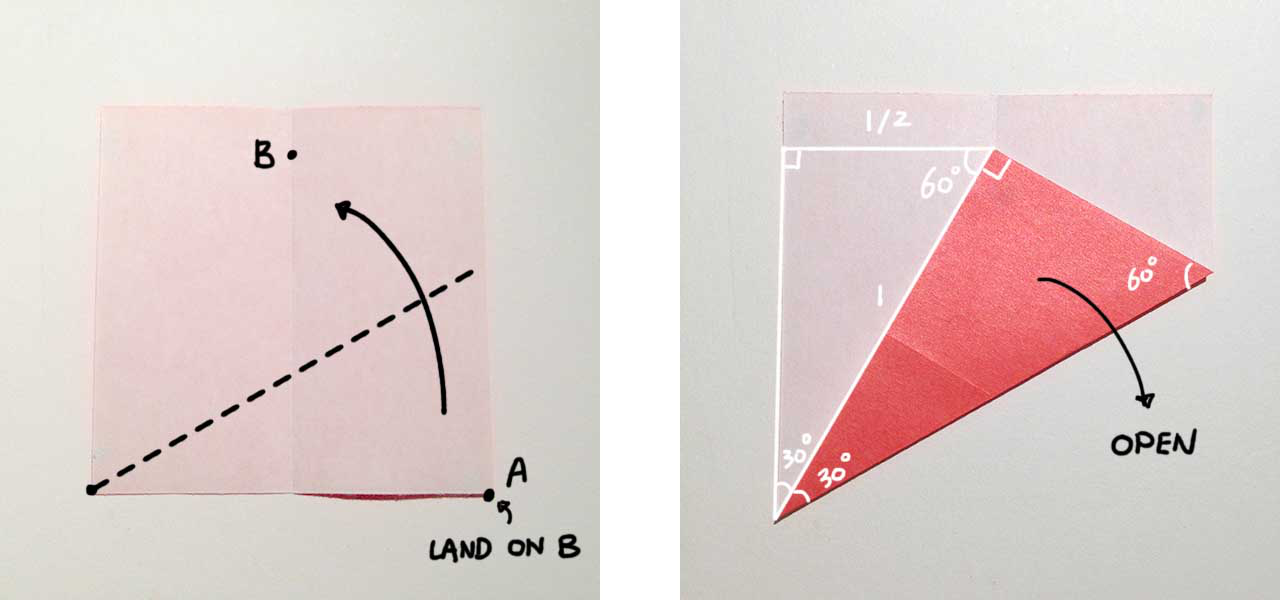
Get your paper ready, colored side down. Fold the right part left to make the paper in half. Crease and open. Youll see a lot of steps just like this: Crease and open. It seems like an undo operation to what youve just done but these steps are definitely not useless. Origami needs geometry to fold certain shapes. Usually it uses creases as a reference to the following steps.

Step 1
Using the bottom-left corner as a pivot, fold the bottom-right corner up. Make it land on the crease made in Step 0. Crease and open. You may find our first 60° angle in the shape. Do the same folding on the opposite side.
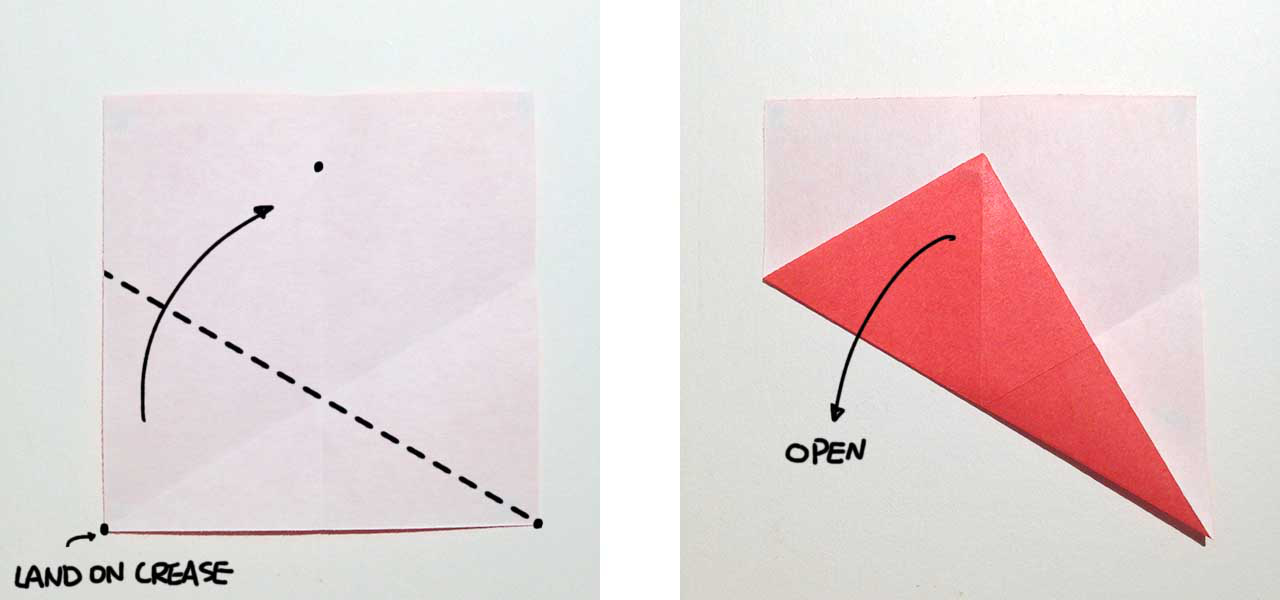
Step 2
Now we have three creases intersecting in a single point. Fold bottom-left and bottom-right corners to the intersection. Crease and open. Two new intersections appeared on the bottom of the square. Fold the left and right edge to the center, make the corners land on the new intersections. For the first time, we dont need to open the folding. The width of the current shape is the length of the longer diagonal of our final rhombus.

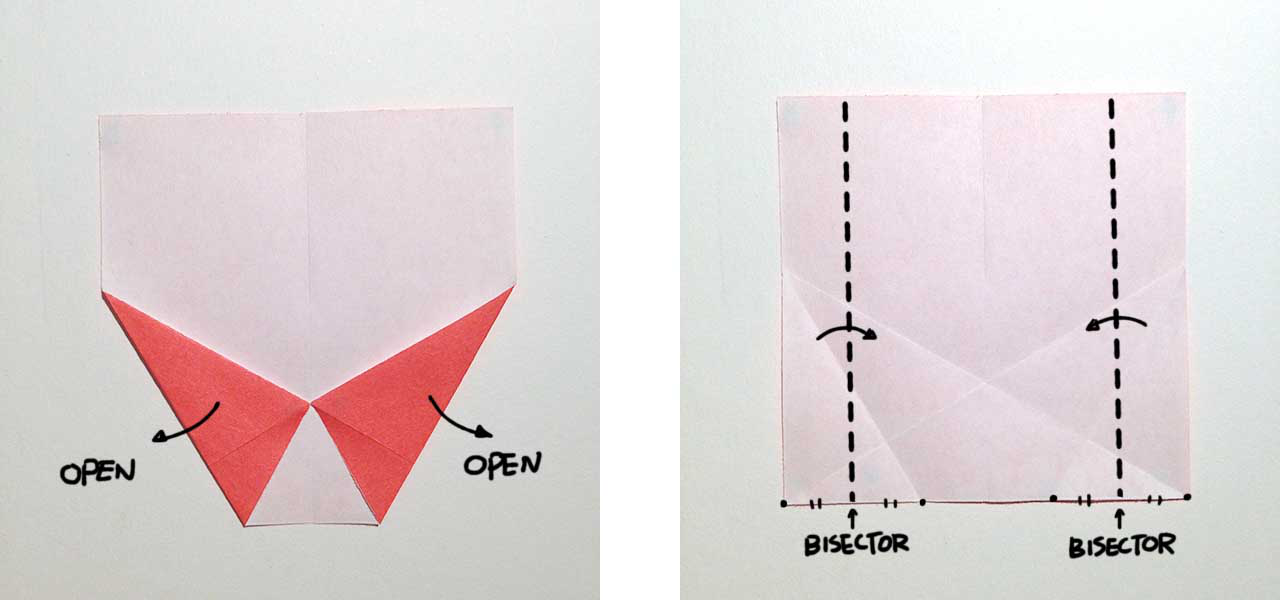
Step 3
Find the intersection of the right edge and the crease made in Step 1. Using the intersection as a pivot, fold the top-right corner down so that the edge is aligned with the crease marked in the picture. Crease and open. Fold the opposite side down in the same way, but dont unfold this time. Fold the triangle upward.


Step 4
Pinch the top layer and pull out. Fold the bottom-right up using the crease made in Step 1. Do it again in the opposite direction: Fold the triangle down, pinch the top layer and pull out.


Step 5
Fold the right part to the left. Crease and open. The following movement is a little bit hard to describe. We need to pinch the marked point, pull to the left, using the center line crease. The animated graphic below might be easier to follow. Fold the triangle upward.

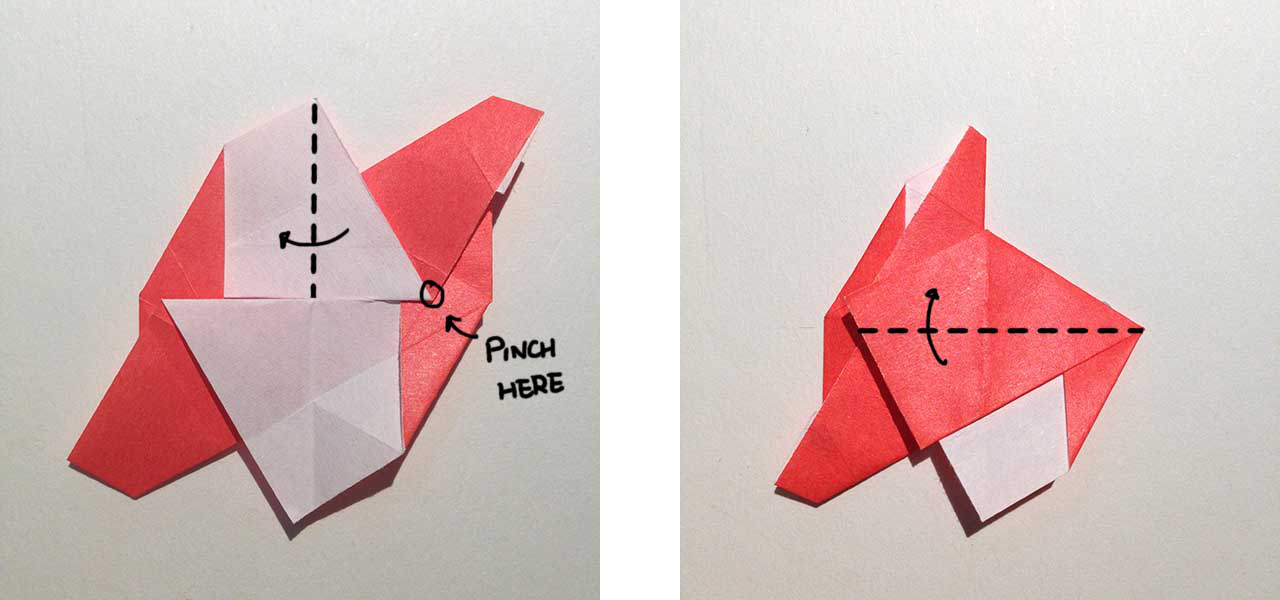

Step 6
Fold the shaded triangle inward, insert it under the layer below. Repeat Step 5-6 in the opposite direction: Pull the left part to the right, fold the triangle down and fold the shaded part inward.

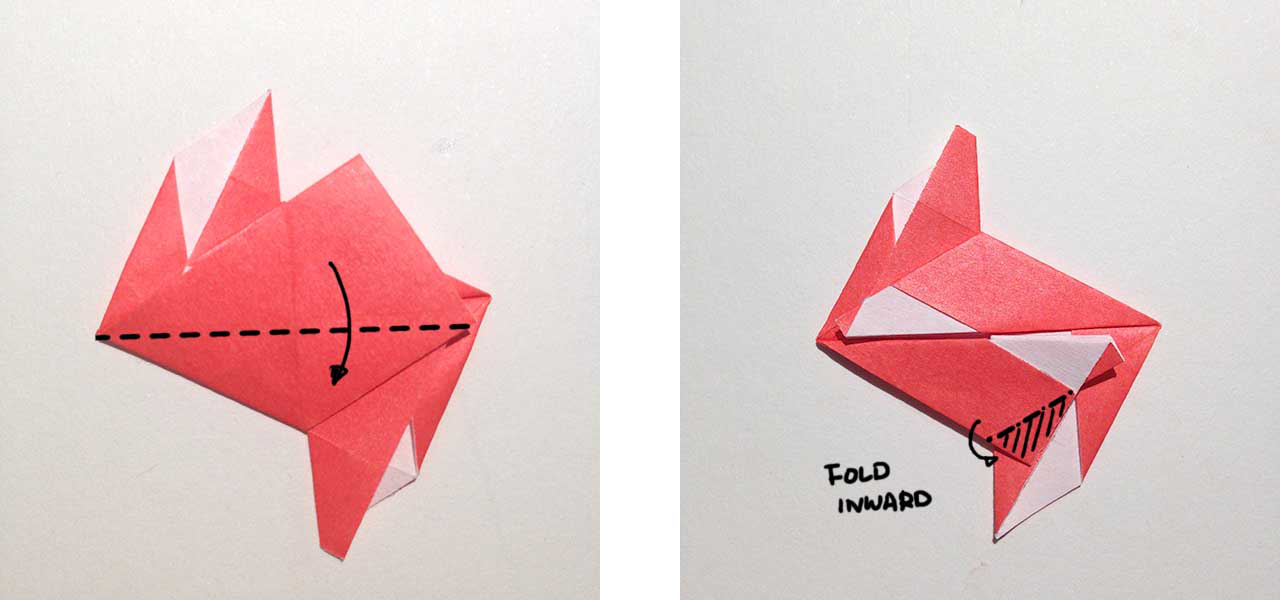
Step 7
Insert the marked parts one layer down. And its done! Turn over and youll see a perfect rhombus with a 60° angle.


Assembly Method
Spikey (1.5h to finish)
Step 0
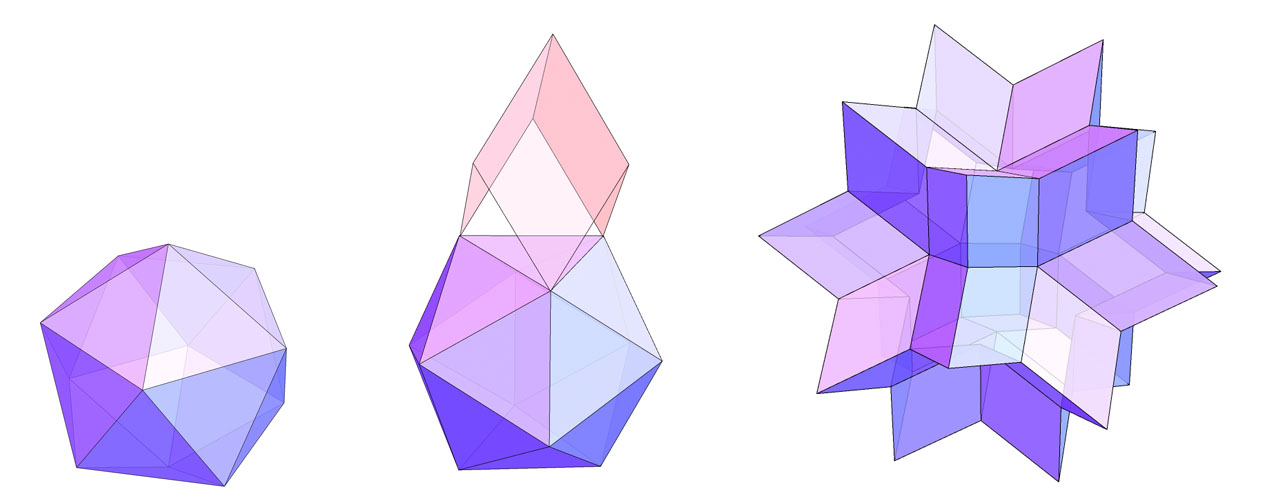
Get your 30 units ready. Before we start, we need to know how to assemble two units. Find two pockets and two joints on the unit. Fold the unit in half, and fold both joints forward as shown in the picture. When assembling, insert one joint of the unit into one pocket of the other unit until it reaches the end.

Step 1
Assemble your first 5 units. You may follow the color I used in the picture, if you wish to have a similar colored model. Our final model will have a lot (twelve) of this star-liked component.

Step 2
Attach 5 more units to the existing model. Join each new unit with two existing units on the 5-unit-structure to form a spike. We will construct twenty spikes on our final model. These 5 units added in this step are our second layer. Now we have 10 assembled units.

Step 3
We need 10 units on our third layer. Insert two units between each two units on Layer 2. Since there are 5 units on Layer 2, we will need 10 units for Layer 3. Observe the model, you will find two kinds of vertexes. The concave ones should have five units around, forming a star-liked structure, while the convex ones have three units forming a spike.

Step 4
Turn the model over, connect each two adjacent units on Layer 3 to form a spike. Assemble 5 new units to Layer 3 to form 5 more spikes.

Step 5
Assemble 5 last units on the top layer to form a star-liked-structure. The final insertion might get difficult, you can fold the joint in half to make it shorter. Dont worry, the final model will still be steady enough. ? 
Wolfram|Alpha (2.5h to finish)
Step 0
Wolfram|Alpha logo is a rhombic hexecontahedron, that means each face is a rhombus. The insertion of the units are slightly different. We dont need to fold the unit in half, just insert the joint into the pocket of another unit. Prepare 60 red units. You may insert every 5 units together to make counting easier.

Step 1
Use 5 units to form a star. Make 12 stars using all 60 units. Connect two stars together, every two stars have two connected vertices. ? 
Step 2
Follow the rule of each two stars have two connected vertices, assemble the stars. Every 6 stars can form a hemisphere. Connect two hemispheres together. And its done!
