For reference, the related discussion is probably http://community.wolfram.com/groups/-/m/t/415464.

Thank you, that is much better.

I played around with this and I can say a couple of things.

(1) This next variant works as expected.

threshold = FindRoot[Integrate[
    fSum[y] /. Catenate[{setb, setp}], {y, detThresh, \[Infinity]}, 
    Assumptions -> Element[detThresh, Reals]] == pfa, {detThresh, initThresh}]

I suspect this means FindRoot has a problem in this case with the ConditionalExpression result from that Integrate (without the Assumptions specification). Offhand I do not know why. I'll poke around if I get a chance.

(2) As I believe was noted in a related thread, it might be better to define the function as a "black box" that only exists when given explicitly numeric input. That would forestall any issues FindRoot might be having with the symbolic Integrate result.

Upshot: there may be a bug, and there are definitely workarounds.

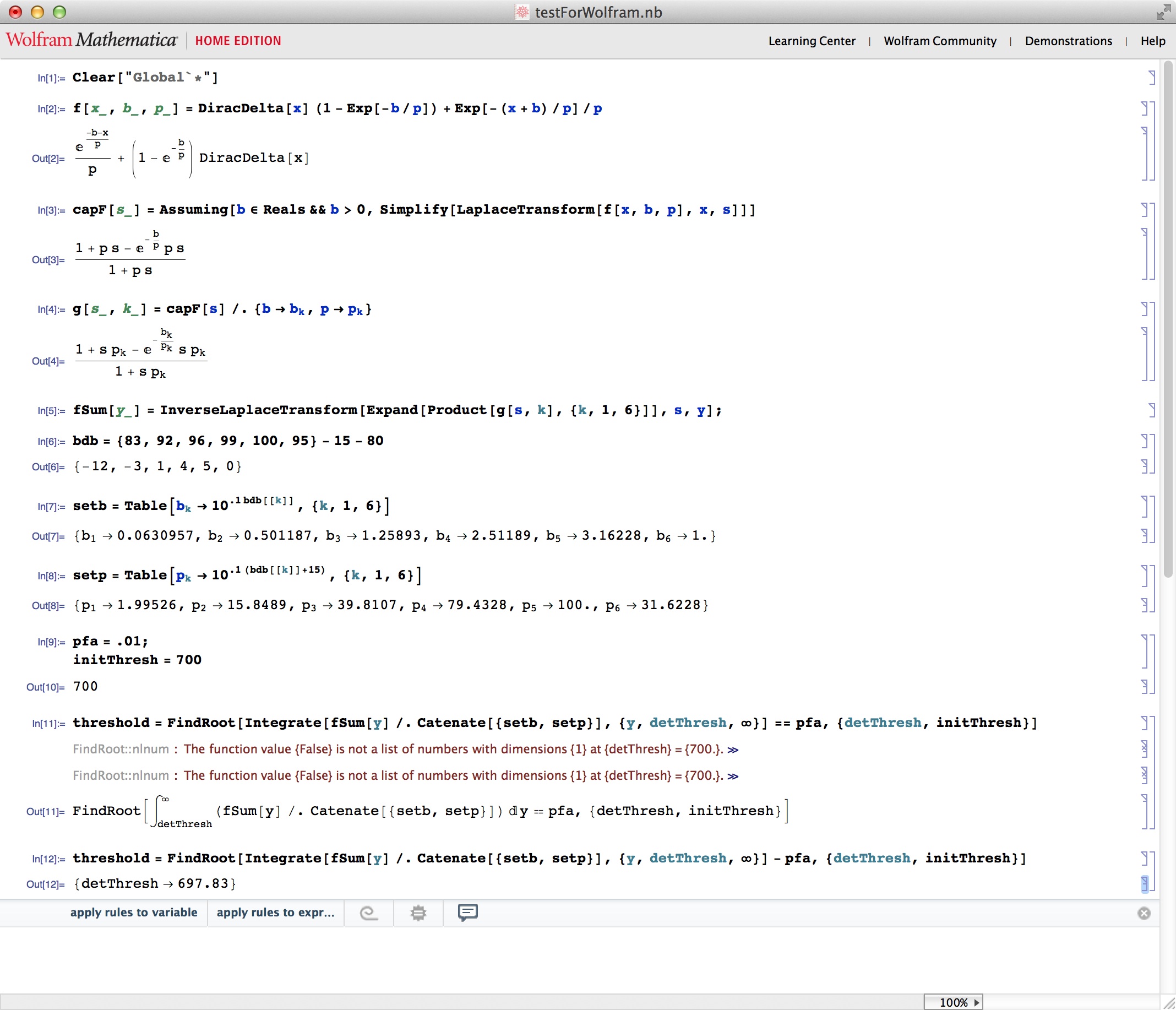
Daniel,

Sorry for the terse initial post. I mistakenly assumed that the remainder of the code was irrelevant, Here is an example of the complete code.

In[1]:= Clear["Global`*"]

In[2]:= f[x_, b_, p_] = 
 DiracDelta[x] (1 - Exp[-b/p]) + Exp[-(x + b)/p]/p

Out[2]= E^((-b - x)/p)/p + (1 - E^(-(b/p))) DiracDelta[x]

In[3]:= capF[s_] = 
 Assuming[b \[Element] Reals && b > 0, 
  Simplify[LaplaceTransform[f[x, b, p], x, s]]]

Out[3]= (1 + p s - E^(-(b/p)) p s)/(1 + p s)

In[4]:= g[s_, k_] = 
 capF[s] /. {b -> Subscript[b, k], p -> Subscript[p, k]}

Out[4]= (1 + s Subscript[p, k] - 
 E^(-(Subscript[b, k]/Subscript[p, k])) s Subscript[p, k])/(1 + 
 s Subscript[p, k])

In[5]:= fSum[y_] = 
  InverseLaplaceTransform[Expand[Product[g[s, k], {k, 1, 6}]], s, y];

In[6]:= bdb = {83, 92, 96, 99, 100, 95} - 15 - 80  

Out[6]= {-12, -3, 1, 4, 5, 0}

In[7]:= setb = Table[Subscript[b, k] -> 10^(.1 bdb[[k]]), {k, 1, 6}]

Out[7]= {Subscript[b, 1] -> 0.0630957, Subscript[b, 2] -> 0.501187, 
 Subscript[b, 3] -> 1.25893, Subscript[b, 4] -> 2.51189, 
 Subscript[b, 5] -> 3.16228, Subscript[b, 6] -> 1.}

In[8]:= setp = 
 Table[Subscript[p, k] -> 10^(.1 (bdb[[k]] + 15)), {k, 1, 6}] 

Out[8]= {Subscript[p, 1] -> 1.99526, Subscript[p, 2] -> 15.8489, 
 Subscript[p, 3] -> 39.8107, Subscript[p, 4] -> 79.4328, 
 Subscript[p, 5] -> 100., Subscript[p, 6] -> 31.6228}

In[9]:= pfa = .01;
initThresh = 700

Out[10]= 700

In[11]:= threshold = 
 FindRoot[Integrate[
    fSum[y] /. Catenate[{setb, setp}], {y, detThresh, \[Infinity]}] ==
    pfa, {detThresh, initThresh}]

During evaluation of In[11]:= FindRoot::nlnum: The function value {False} is not a list of numbers with dimensions {1} at {detThresh} = {700.}. >>

During evaluation of In[11]:= FindRoot::nlnum: The function value {False} is not a list of numbers with dimensions {1} at {detThresh} = {700.}. >>

Out[11]= FindRoot[\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(detThresh\), \
\(\[Infinity]\)]\(\((fSum[y] /.  
      Catenate[{setb, setp}])\) \[DifferentialD]y\)\) == 
  pfa, {detThresh, initThresh}]

In[12]:= threshold = 
 FindRoot[Integrate[
    fSum[y] /. Catenate[{setb, setp}], {y, detThresh, \[Infinity]}] - 
   pfa, {detThresh, initThresh}]
   {detThresh -> 697.83}

The notebook doesn't look quite like the code above so I am also including an image. If it would help I can also attach the file.